3. Medidas de Tendencia Central

Las medidas de tendencia central resumen en un único valor representativo el centro de un conjunto de datos. Permiten entender rápidamente dónde se agrupan los valores. Las tres más importantes son:

Media (o promedio aritmético)

Es la medida más conocida. Se calcula sumando todos los valores del conjunto de datos y dividiendo el resultado por el número total de valores. Es el "centro de gravedad" de los datos.

• Ventaja: Utiliza todos los valores en el cálculo, por lo que es una representación completa del conjunto.
• Desventaja: Es muy sensible a valores extremos (outliers). Un valor muy alto o muy bajo puede "arrastrar" la media y hacer que no sea representativa del valor típico.

Mediana

Es el valor que se encuentra exactamente en el medio del conjunto de datos, una vez que estos han sido ordenados de menor a mayor. Si hay un número par de datos, la mediana es el promedio de los dos valores centrales.

• Ventaja: Es robusta frente a valores extremos. Como solo le importa la posición central, un outlier no afecta su valor significativamente, lo que la hace más representativa en distribuciones asimétricas.
• Desventaja: No utiliza toda la información del conjunto de datos, solo los valores centrales.

Moda

Es el valor que aparece con mayor frecuencia en el conjunto de datos. Un conjunto puede tener una moda (unimodal), dos (bimodal), varias (multimodal) o ninguna.

• Ventaja: Es la única medida de tendencia central que se puede utilizar con datos categóricos (no numéricos), como "color de ojos" o "marca de coche". También es útil para identificar los picos en una distribución.
• Desventaja: Puede no existir o no ser única. En conjuntos de datos pequeños o con poca repetición, puede no ser un buen representante del centro.

3.1 Media aritmética

Fórmula: Media = (∑x_i) / n

Calcular la media

# Script 1: Media con NumPy y Pandas
import numpy as np
import pandas as pd

ingresos = [8200, 9100, 7500, 20000, 8300, 8700]

media_numpy = np.mean(ingresos)
media_pandas = pd.Series(ingresos).mean()

print(f"Media con NumPy: {media_numpy:.2f}")
print(f"Media con Pandas: {media_pandas:.2f}")

👉 Notar que el 20.000 sube mucho la media: es sensible a outliers.

3.2 Mediana

La mediana divide al dataset en dos partes con igual número de observaciones.

Mediana

# Script 2: Mediana con NumPy y Pandas
import numpy as np
import pandas as pd

ingresos = [8200, 9100, 7500, 20000, 8300, 8700]

mediana_numpy = np.median(ingresos)
mediana_pandas = pd.Series(ingresos).median()

print(f"Mediana con NumPy: {mediana_numpy}")
print(f"Mediana con Pandas: {mediana_pandas}")

👉 La mediana en este caso refleja mejor el “valor típico” porque ignora el efecto del outlier.

3.3 Moda

La moda es el valor que más se repite. En Python se puede calcular con SciPy o con Pandas.

Moda

# Script 3: Moda con SciPy y Pandas
import pandas as pd
from scipy import stats

datos = [5, 6, 6, 7, 7, 7, 8, 9, 9]

moda_scipy = stats.mode(datos, keepdims=True)
moda_pandas = pd.Series(datos).mode()

print(f"Moda con SciPy: {moda_scipy.mode[0]} (ocurre {moda_scipy.count[0]} veces)")
print(f"Moda con Pandas: {list(moda_pandas)}")

👉 Con Pandas puede haber múltiples modas (empates).

3.4 Comparación entre media, mediana y moda

Ejemplo con outliers

# Script 4: Comparación de media, mediana y moda
import numpy as np
import pandas as pd

ingresos = [8200, 9100, 7500, 8300, 8700, 8600, 20000]  # con un outlier

serie = pd.Series(ingresos)

print("Media  :", serie.mean())
print("Mediana:", serie.median())
print("Moda   :", list(serie.mode()))

Interpretación:

• Media ≈ 10.242 → inflada por el valor extremo.
• Mediana ≈ 8.700 → más representativa.
• Moda = 8.200/8.300/etc. (según los datos, útil si se repite).

3.5 Visualización

Gráfico con media, mediana y moda

# Script 5: Visualización de media, mediana y moda
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

ingresos = [8200, 9100, 7500, 8300, 8700, 8600, 20000]
serie = pd.Series(ingresos)

media = serie.mean()
mediana = serie.median()
moda = serie.mode().iloc[0]

sns.histplot(serie, bins=10, kde=True, color="skyblue")

plt.axvline(media, color="red", linestyle="--", label=f"Media: {media:.0f}")
plt.axvline(mediana, color="green", linestyle="-.", label=f"Mediana: {mediana:.0f}")
plt.axvline(moda, color="purple", linestyle=":", label=f"Moda: {moda}")

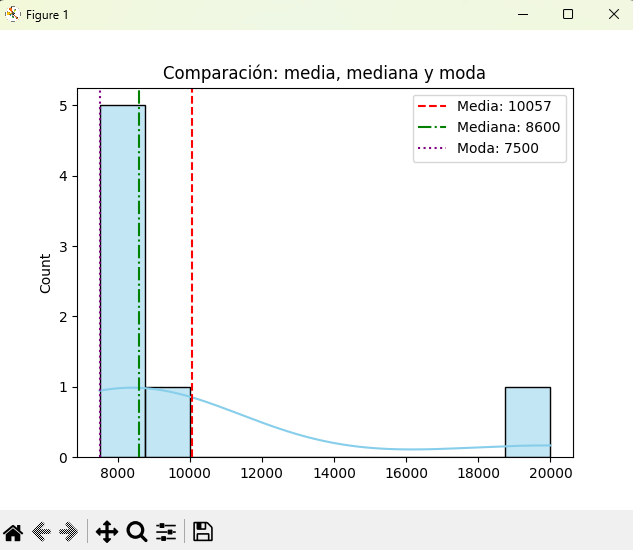
plt.title("Comparación: media, mediana y moda")
plt.legend()
plt.show()

👉 Se ve cómo la media se desplaza hacia la derecha por el outlier, mientras la mediana queda más centrada.