4. Medidas de dispersión

Las medidas de dispersión son cruciales porque nos dicen qué tan dispersos o concentrados están los datos alrededor de su centro (como la media). Conocer solo la tendencia central no es suficiente; dos conjuntos de datos pueden tener la misma media pero una variabilidad completamente distinta.

Rango

Es la medida más simple de dispersión. Se calcula como la diferencia entre el valor máximo y el valor mínimo del conjunto de datos.

• Fórmula: Rango = Valor Máximo - Valor Mínimo
• Ventaja: Muy fácil de calcular e interpretar.
• Desventaja: Es extremadamente sensible a los valores atípicos (outliers), ya que solo depende de los dos valores extremos del conjunto.

Varianza (σ²)

La varianza mide la dispersión promedio de los datos respecto a la media. Para cada punto, calcula la distancia a la media y la eleva al cuadrado (para evitar números negativos y magnificar las diferencias grandes). La varianza es el promedio de estas diferencias al cuadrado.

• Concepto: Un valor pequeño indica que los datos están agrupados cerca de la media. Un valor grande indica que están más dispersos.
• Desventaja: Sus unidades están al cuadrado (ej. "dólares²"), lo que dificulta su interpretación directa en el contexto de los datos originales.
• Nota: Existe una varianza poblacional (cuando tienes datos de toda la población, se divide por N) y una muestral (cuando usas una muestra, se divide por n-1 para corregir el sesgo).

Desviación Estándar (σ)

Es la medida de dispersión más utilizada y es simplemente la raíz cuadrada de la varianza. Su gran ventaja es que vuelve a las unidades originales de los datos.

• Interpretación: Nos dice, en promedio, qué tan lejos está cada punto de la media. Una desviación estándar baja significa que los datos están muy agrupados; una alta significa que están muy extendidos.
• Ejemplo: Si el ingreso medio es de $5000 con una desviación estándar de $500, la mayoría de los ingresos se agrupan entre $4500 y $5500 (siguiendo la regla empírica para distribuciones normales).

Coeficiente de Variación (CV)

Es una medida de dispersión relativa, que no tiene unidades. Se calcula dividiendo la desviación estándar por la media. Es especialmente útil para comparar la variabilidad de dos o más conjuntos de datos que tienen diferentes escalas o unidades.

• Fórmula: CV = (Desviación Estándar / Media)
• Uso: ¿Qué es más variable, el peso de los elefantes o el de los ratones? La desviación estándar del peso de los elefantes será mucho mayor, pero el CV podría mostrar que, en relación con su peso medio, los ratones son más variables.

Rango

import numpy as np

datos = [12, 15, 20, 22, 29, 30, 45, 50]

rango = np.max(datos) - np.min(datos)
print("Rango:", rango)

Varianza

import numpy as np

datos = [12, 15, 20, 22, 29, 30, 45, 50]

# Varianza poblacional (ddof=0) y muestral (ddof=1)
varianza_poblacional = np.var(datos, ddof=0)
varianza_muestral = np.var(datos, ddof=1)

print("Varianza poblacional:", f"{varianza_poblacional:.2f}")
print("Varianza muestral:", f"{varianza_muestral:.2f}")

Desviación estándar

import numpy as np

datos = [12, 15, 20, 22, 29, 30, 45, 50]

desvio_poblacional = np.std(datos, ddof=0)
desvio_muestral = np.std(datos, ddof=1)

print("Desviación estándar poblacional:", f"{desvio_poblacional:.2f}")
print("Desviación estándar muestral:", f"{desvio_muestral:.2f}")

Coeficiente de variación

import numpy as np

datos = [12, 15, 20, 22, 29, 30, 45, 50]

media = np.mean(datos)
desvio = np.std(datos, ddof=1)

coef_variacion = desvio / media
print("Coeficiente de variación:", f"{coef_variacion:.2f}")

👉 El CV es adimensional. Ejemplo de interpretación:

• CV bajo (< 0.2): datos homogéneos.
• CV alto (> 0.5): datos muy dispersos.

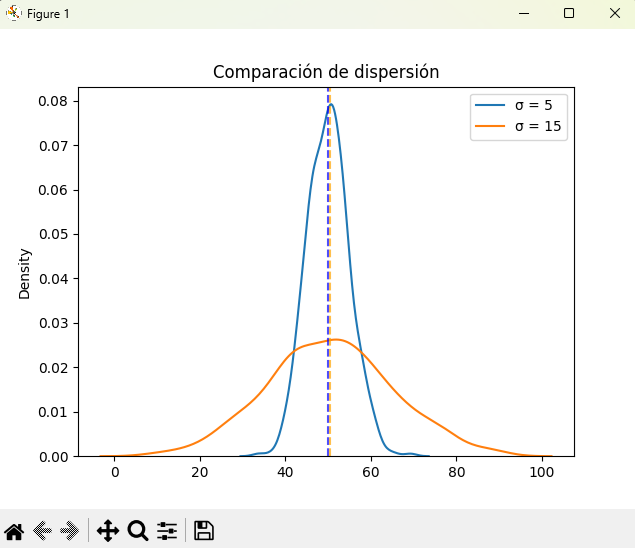
Comparación visual

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

np.random.seed(42)
a = np.random.normal(50, 5, 500)   # baja dispersión
b = np.random.normal(50, 15, 500)  # alta dispersión

sns.kdeplot(a, label="σ = 5")
sns.kdeplot(b, label="σ = 15")
plt.axvline(np.mean(a), color="blue", linestyle="--", alpha=0.7)
plt.axvline(np.mean(b), color="orange", linestyle="--", alpha=0.7)
plt.title("Comparación de dispersión")
plt.legend()
plt.show()

Explicación de np.random.normal:

Esta función de NumPy genera números aleatorios que siguen una distribución normal (o "curva de campana"). Los parámetros que usamos son:

• loc: La media (mean) de la distribución. En nuestro caso es 50 para ambos grupos, por eso sus centros son iguales.
• scale: La desviación estándar (standard deviation). Controla la "anchura" de la curva. Para el grupo a es 5 (baja dispersión), por lo que los datos están más concentrados. Para el grupo b es 15 (alta dispersión), lo que genera datos mucho más extendidos.
• size: El número de muestras a generar. En ambos casos, creamos un array con 500 números.

👉 Ambos grupos tienen la misma media (~50), pero la curva naranja (σ=15) es mucho más ancha → mayor variabilidad.