5. Medidas de posición

Las medidas de posición, también conocidas como cuantiles, son puntos tomados a intervalos regulares de un conjunto de datos ordenado. Su función es dividir la distribución de los datos en partes iguales para entender dónde se ubica un valor específico en relación con el resto.

Cuartiles (Q1, Q2, Q3)

Dividen el conjunto de datos en cuatro partes iguales, donde cada parte contiene el 25% de las observaciones.

  • Q1 (Primer Cuartil): El 25% de los datos es menor o igual a este valor.
  • Q2 (Segundo Cuartil): El 50% de los datos es menor o igual a este valor. Es idéntico a la mediana.
  • Q3 (Tercer Cuartil): El 75% de los datos es menor o igual a este valor.
  • El Rango Intercuartílico (IQR), que es Q3 - Q1, representa el 50% central de los datos y es una medida de dispersión muy robusta frente a outliers.

Deciles (D1, D2, ..., D9)

Dividen el conjunto de datos en diez partes iguales (cada una con el 10% de los datos).

  • D1: El 10% de los datos está por debajo de este valor.
  • D5: Coincide con el Q2 y la mediana (50%).
  • D9: El 90% de los datos está por debajo de este valor.

Percentiles (P1, P2, ..., P99)

Es la división más fina, en cien partes iguales. Un percentil indica el porcentaje de datos que son iguales o menores que un determinado valor.

  • Ejemplo común: Si la nota de tu examen está en el "percentil 90", significa que has superado al 90% de los demás estudiantes.
  • Relación: P25 es lo mismo que Q1, P50 es la mediana (Q2), y P75 es Q3.

👉 Son muy útiles para detectar asimetrías y valores atípicos (outliers).

Cuartiles con NumPy y Pandas

import numpy as np
import pandas as pd

datos = [15, 18, 21, 24, 30, 35, 40, 42, 50, 60]

serie = pd.Series(datos)

q1 = serie.quantile(0.25)
q2 = serie.median()   # equivalente a Q2
q3 = serie.quantile(0.75)

print("Q1 (25%):", q1)
print("Q2 (50%, mediana):", q2)
print("Q3 (75%):", q3)

Deciles y Percentiles

import numpy as np
import pandas as pd

datos = np.random.randint(1, 100, 20)
serie = pd.Series(datos)

# Deciles
deciles = [serie.quantile(i/10) for i in range(1, 10)]
print("Deciles:", deciles)

# Percentiles 10, 25, 50, 75, 90
percentiles = [10, 25, 50, 75, 90]
print("\nPercentiles con NumPy:")
for p in percentiles:
    print(f"P{p}:", np.percentile(datos, p))

Resumen completo con múltiples cuantiles

import numpy as np
import pandas as pd

np.random.seed(42)
datos = np.random.normal(100, 15, 200)  # notas de examen simuladas
serie = pd.Series(datos)

resumen = serie.quantile([0.1, 0.25, 0.5, 0.75, 0.9])
print("Resumen de cuantiles:\n", resumen)

Visualización de cuartiles con boxplot

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

np.random.seed(0)
datos = np.random.normal(50, 10, 300)

sns.boxplot(x=datos)
plt.title("Boxplot con cuartiles y outliers")
plt.show()
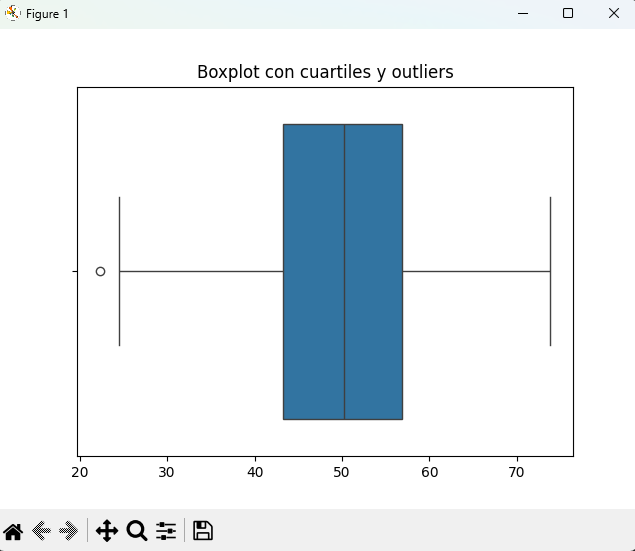
Visualización de un boxplot con sus componentes: cuartiles, mediana y outliers

👉 En el boxplot:

  • Caja = rango intercuartílico (Q1 a Q3).
  • Línea dentro = mediana (Q2).
  • “Bigotes” = valores dentro de 1.5 * IQR.
  • Puntos fuera = outliers.
Volver al inicio