7. Distribuciones de datos en Python

Una distribución de datos describe cómo se reparten los valores de una variable. Visualizarla es fundamental para entender su forma, centro y dispersión. En Python, Seaborn y Matplotlib ofrecen herramientas excelentes para este propósito.

Las más importantes son:

Histogramas (histplot)

Es la herramienta fundamental para visualizar la distribución de una variable numérica continua. Funciona de la siguiente manera:

• Divide todo el rango de valores de los datos en una serie de intervalos o "contenedores" (bins).
• Cuenta cuántos valores de los datos caen dentro de cada intervalo.
• Dibuja una barra para cada intervalo, donde la altura de la barra representa la frecuencia (el número de valores).
• Clave: La elección del número de bins es importante. Pocos bins pueden ocultar detalles, mientras que demasiados pueden generar un gráfico ruidoso y difícil de leer.

KDE (Kernel Density Estimation)

Es una estimación de la "curva de densidad de probabilidad" de los datos. Se puede pensar como una versión suavizada y continua de un histograma.

• A diferencia del histograma, no agrupa los datos en bins. En su lugar, coloca una pequeña curva (kernel) en cada punto de datos y luego suma todas esas curvas para obtener una única curva final.
• Ventaja: Permite ver la forma de la distribución de manera más clara, sin la distracción de los bins, facilitando la identificación de picos (modas) y asimetría.

Boxplots (Diagramas de Caja y Bigotes)

Ofrecen un resumen visual y conciso de la distribución basado en cuartiles. Son excelentes para comparar distribuciones entre diferentes grupos y para detectar valores atípicos.

• La caja central contiene el 50% de los datos (el Rango Intercuartílico o IQR, de Q1 a Q3).
• La línea dentro de la caja marca la mediana (Q2).
• Los "bigotes" se extienden desde la caja para mostrar el resto de la distribución, generalmente hasta 1.5 veces el IQR.
• Los puntos individuales más allá de los bigotes se consideran valores atípicos (outliers).

Histograma simple con Seaborn

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

np.random.seed(0)
datos = np.random.normal(50, 10, 300)

sns.histplot(datos, bins=15, color="skyblue")
plt.title("Histograma simple")
plt.xlabel("Valores")
plt.ylabel("Frecuencia")
plt.show()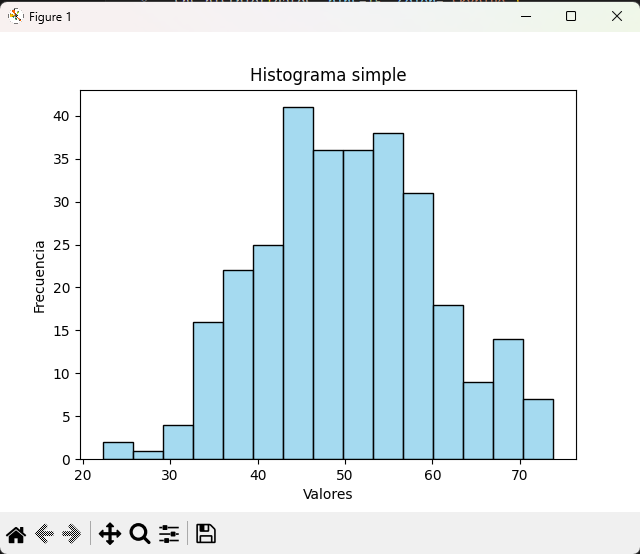

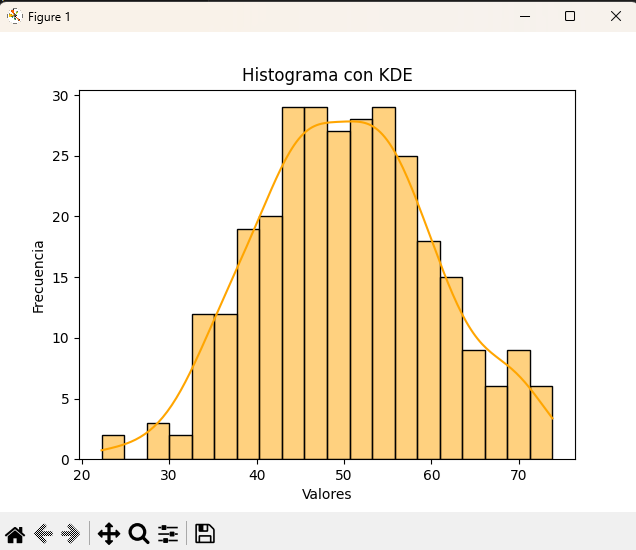
Histograma con densidad (KDE)

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

np.random.seed(0)
datos = np.random.normal(50, 10, 300)

sns.histplot(datos, bins=20, kde=True, color="orange")
plt.title("Histograma con KDE")
plt.xlabel("Valores")
plt.ylabel("Frecuencia")
plt.show()

👉 El KDE permite ver mejor la forma de la distribución (simétrica, sesgada, etc.).

Distribuciones suavizadas con sns.kdeplot

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

np.random.seed(0)
datos = np.random.normal(50, 10, 300)

sns.kdeplot(datos, fill=True, color="purple")
plt.title("Distribución suavizada con KDE")
plt.xlabel("Valores")
plt.show()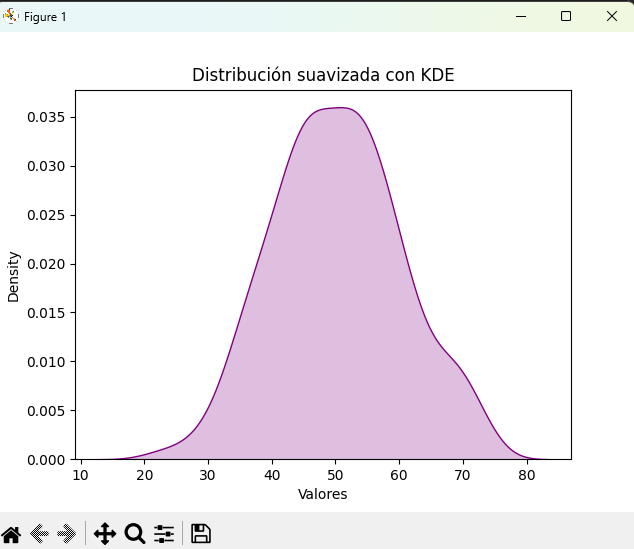

Boxplot (resumen y outliers)

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

np.random.seed(0)
datos = np.random.normal(50, 10, 300)

sns.boxplot(x=datos, color="lightgreen")
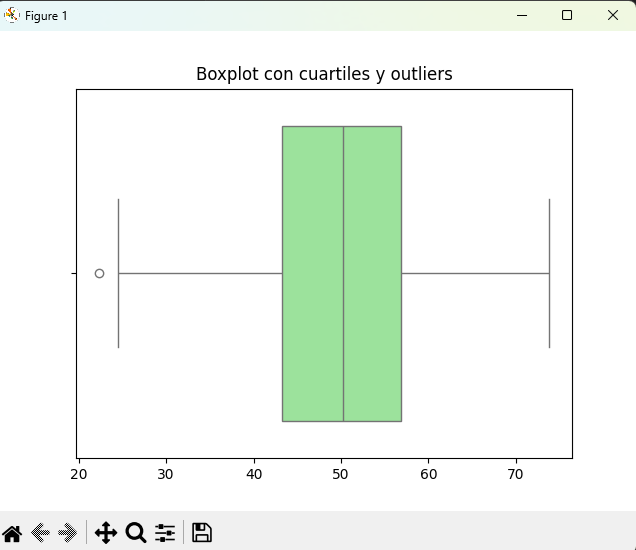
plt.title("Boxplot con cuartiles y outliers")
plt.show()

👉 En el boxplot:

• Caja: rango intercuartílico (Q1 a Q3).
• Línea central: mediana.
• Bigotes: rango esperado de datos.
• Puntos fuera: outliers.

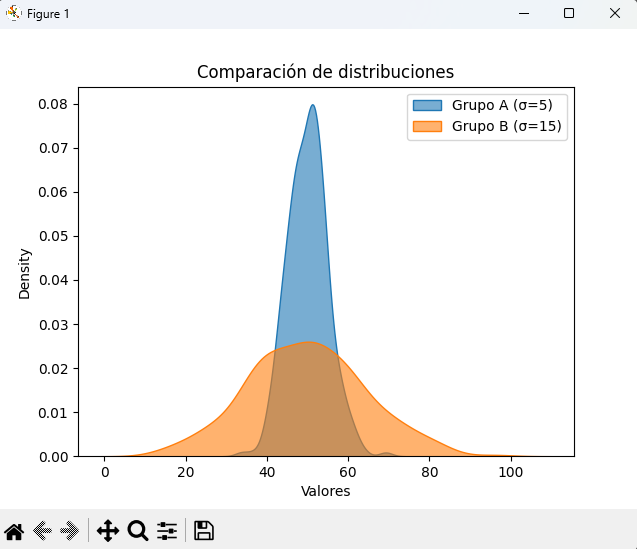
Comparación de dos distribuciones

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

np.random.seed(42)
grupo_a = np.random.normal(50, 5, 300)   # menor dispersión
grupo_b = np.random.normal(50, 15, 300)  # mayor dispersión

sns.kdeplot(grupo_a, fill=True, label="Grupo A (σ=5)", alpha=0.6)
sns.kdeplot(grupo_b, fill=True, label="Grupo B (σ=15)", alpha=0.6)
plt.title("Comparación de distribuciones")
plt.xlabel("Valores")
plt.legend()
plt.show()

👉 Ambas distribuciones tienen la misma media (~50) pero diferente desviación estándar → el grupo B es mucho más disperso.