8. Asimetría y curtosis

8.1 Asimetría (Skewness)

La asimetría mide si una distribución está inclinada hacia la izquierda o hacia la derecha respecto a la media.

• Asimetría = 0 → distribución simétrica (ej. Normal perfecta).
• Asimetría > 0 → sesgo a la derecha (cola larga hacia valores altos).
• Asimetría < 0 → sesgo a la izquierda (cola larga hacia valores bajos).

👉 Interpretación rápida:

• |skew| < 0.5 → distribución aproximadamente simétrica.
• 0.5 ≤ |skew| < 1 → asimetría moderada.
• |skew| ≥ 1 → asimetría fuerte.

8.2 Curtosis (Kurtosis)

La curtosis mide el grado de “apuntamiento” o “aplanamiento” de la distribución respecto a la normal.

• Curtosis normal = 0 (mesocúrtica, distribución normal estándar).
• Curtosis > 0 → leptocúrtica (pico más alto, colas más pesadas).
• Curtosis < 0 → platicúrtica (más plana, colas más ligeras).

👉 Ojo: SciPy devuelve exceso de curtosis (comparado con normal).

8.3 Cálculo con SciPy

import numpy as np
from scipy.stats import skew, kurtosis

np.random.seed(42)

# Distribuciones simuladas
normal = np.random.normal(0, 1, 1000)        # simétrica
sesgada = np.random.exponential(1, 1000)     # sesgo a la derecha

print("Distribución normal:")
print("Asimetría:", skew(normal))
print("Curtosis:", kurtosis(normal), "\n")

print("Distribución sesgada:")
print("Asimetría:", skew(sesgada))
print("Curtosis:", kurtosis(sesgada))
                        

La distribución exponencial es un ejemplo clásico de una distribución con un fuerte sesgo a la derecha. Se utiliza comúnmente para modelar el tiempo hasta que ocurre un evento (por ejemplo, el tiempo entre dos llamadas a un call center).

En este código:

• np.random.exponential(1, 1000) genera 1000 números aleatorios que siguen esta distribución.
• La mayoría de estos números serán pequeños y estarán cerca de cero.
• Sin embargo, habrá unos pocos valores mucho más grandes que se extienden hacia la derecha, creando la característica "cola larga" que produce una asimetría positiva y fuerte.

8.4 Ejemplos con gráficos

Distribución normal vs. sesgada

import numpy as np
from scipy.stats import skew, kurtosis
import seaborn as sns
import matplotlib.pyplot as plt

np.random.seed(42)
normal = np.random.normal(0, 1, 1000)
sesgada = np.random.exponential(1, 1000)

fig, axes = plt.subplots(1, 2, figsize=(12, 5))

sns.histplot(normal, bins=30, kde=True, ax=axes[0], color="skyblue")
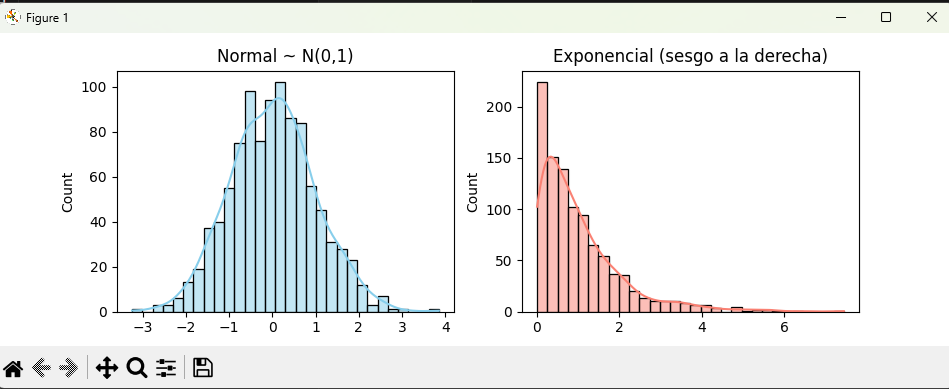
axes[0].set_title("Normal ~ N(0,1)")

sns.histplot(sesgada, bins=30, kde=True, ax=axes[1], color="salmon")
axes[1].set_title("Exponencial (sesgo a la derecha)")

plt.show()
                        

👉 Visualmente:

• La normal es simétrica (skew ≈ 0, kurtosis ≈ 0).
• La exponencial tiene cola a la derecha (skew > 1, curtosis > 0).

Comparación de curtosis

import numpy as np
from scipy.stats import kurtosis
import seaborn as sns
import matplotlib.pyplot as plt

# Distribuciones con diferente curtosis
np.random.seed(1)
baja_curtosis = np.random.uniform(-2, 2, 1000)   # platicúrtica
alta_curtosis = np.random.laplace(0, 1, 1000)    # leptocúrtica

print("Uniforme (platicúrtica): curtosis =", kurtosis(baja_curtosis))
print("Laplace (leptocúrtica): curtosis =", kurtosis(alta_curtosis))

fig, axes = plt.subplots(1, 2, figsize=(12, 5))

sns.histplot(baja_curtosis, bins=30, kde=True, ax=axes[0], color="lightgreen")
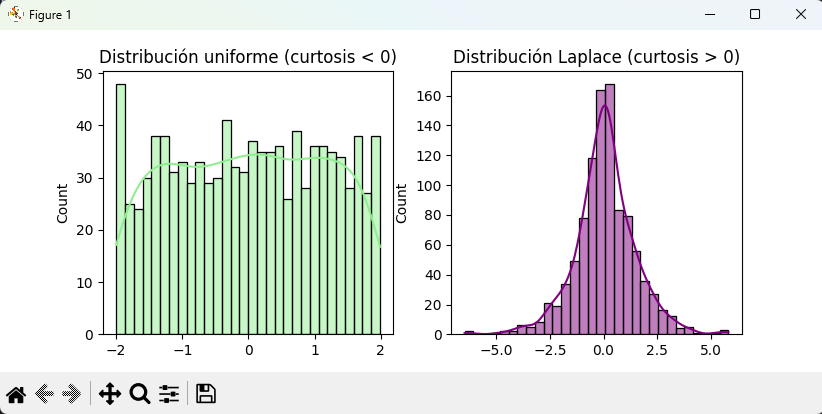
axes[0].set_title("Distribución uniforme (curtosis < 0)")

sns.histplot(alta_curtosis, bins=30, kde=True, ax=axes[1], color="purple")
axes[1].set_title("Distribución Laplace (curtosis > 0)")

plt.show()
                        

👉 Interpretación:

• Uniforme → más plana, curtosis negativa.
• Laplace → más “picuda” y colas pesadas, curtosis positiva.

8.5 Conclusión práctica

Asimetría nos indica hacia dónde se inclina la distribución.

Curtosis nos habla de qué tan “picuda” o “plana” es respecto a la normal.

Son métricas muy útiles para:

• Validar supuestos de normalidad en estadística inferencial.
• Detectar outliers y comportamientos extremos.
• Comparar distribuciones en exploración de datos.