9. Correlación entre variables
La correlación mide el grado y la dirección de la relación lineal o monotónica entre dos variables.
9.1 Covarianza
Indica cómo varían dos variables juntas.
- Positiva → ambas crecen o decrecen a la vez.
- Negativa → una sube mientras la otra baja.
- Depende de las unidades, por lo que no es directamente comparable.
Cov(X,Y) = Σ(xi - x̄)(yi - ȳ) / (n-1)
9.2 Coeficiente de correlación de Pearson
Normaliza la covarianza entre -1 y 1.
- 1 = relación lineal perfecta positiva.
- -1 = relación lineal perfecta negativa.
- 0 = no hay relación lineal (pero puede existir relación no lineal).
9.3 Correlación de Spearman
Basada en rangos, no en valores absolutos.
- Útil para relaciones monotónicas (no necesariamente lineales).
- Menos sensible a outliers.
9.4 Ejemplos en Python
Covarianza y correlación simple
import numpy as np
import pandas as pd
# Simulación de datos
np.random.seed(42)
x = np.random.normal(50, 10, 100)
y = 2 * x + np.random.normal(0, 10, 100) # y depende linealmente de x
df = pd.DataFrame({"X": x, "Y": y})
# Covarianza
print("Matriz de covarianza:\n", np.cov(df["X"], df["Y"]))
# Correlación de Pearson
print("\nCorrelación de Pearson:", df["X"].corr(df["Y"]))
👉 Se espera una correlación alta y positiva, cercana a 1.
Correlación de Spearman
import numpy as np
import pandas as pd
from scipy.stats import spearmanr
np.random.seed(42)
x = np.random.normal(50, 10, 100)
y = 2 * x + np.random.normal(0, 10, 100)
df = pd.DataFrame({"X": x, "Y": y})
coef, p_value = spearmanr(df["X"], df["Y"])
print("Correlación de Spearman:", coef)
Matriz de correlaciones entre múltiples variables
import numpy as np
import pandas as pd
# Dataset con 3 variables
np.random.seed(0)
a = np.random.normal(50, 10, 100)
b = a * 1.5 + np.random.normal(0, 5, 100)
c = np.random.normal(30, 5, 100)
df = pd.DataFrame({"A": a, "B": b, "C": c})
print("Matriz de correlación de Pearson:")
print(df.corr())
Heatmap de correlación con Seaborn
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
np.random.seed(0)
a = np.random.normal(50, 10, 100)
b = a * 1.5 + np.random.normal(0, 5, 100)
c = np.random.normal(30, 5, 100)
df = pd.DataFrame({"A": a, "B": b, "C": c})
corr_matrix = df.corr()
plt.figure(figsize=(6,4))
sns.heatmap(corr_matrix, annot=True, cmap="coolwarm", center=0)
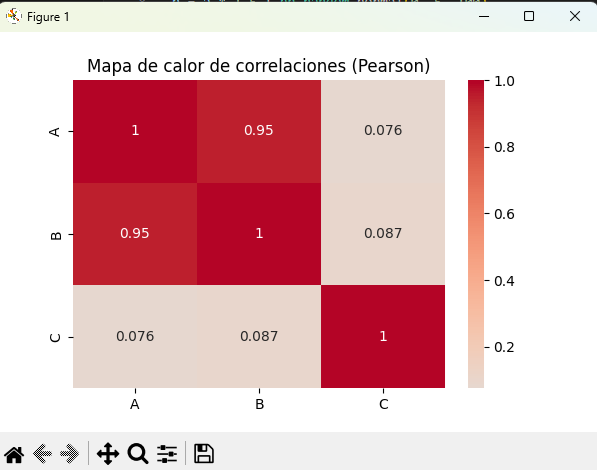
plt.title("Mapa de calor de correlaciones (Pearson)")
plt.show()
👉 El heatmap facilita visualizar relaciones fuertes (positivas o negativas).
Ejemplo de correlación no lineal
import numpy as np
import pandas as pd
# Relación cuadrática: no es lineal
x = np.linspace(-10, 10, 200)
y = x**2 + np.random.normal(0, 5, 200)
df = pd.DataFrame({"X": x, "Y": y})
print("Correlación de Pearson:", df["X"].corr(df["Y"]))
print("Correlación de Spearman:", df["X"].corr(df["Y"], method="spearman"))
👉 Aquí Pearson ≈ 0 (porque no hay relación lineal), pero Spearman ≈ 1 (porque la relación es monotónica creciente en valores absolutos).
9.5 Conclusión práctica
- Covarianza: mide la variación conjunta, pero depende de la escala.
- Pearson: detecta relaciones lineales.
- Spearman: útil en relaciones no lineales y con outliers.
- Mapas de calor: herramienta clave para ver correlaciones entre muchas variables.