10. Ejemplos prácticos en Python
En esta sección, aplicaremos los conceptos de inferencia estadística aprendidos a través de ejemplos prácticos con datasets reales en Python. Utilizaremos librerías como Pandas para la manipulación de datos, SciPy para las pruebas estadísticas y Seaborn/Matplotlib para la visualización.
10.1 Dataset tips (propinas en restaurantes)
El dataset `tips` contiene información sobre propinas dadas en un restaurante, incluyendo el monto de la cuenta, la propina, el sexo del pagador, si era fumador, el día de la semana, la hora y el tamaño de la mesa. Es ideal para explorar relaciones entre variables categóricas y numéricas.
Pregunta de investigación: ¿Existe una diferencia significativa en la propina promedio entre fumadores y no fumadores?
- Hipótesis Nula (H₀): La propina promedio es igual para fumadores y no fumadores (μ_fumador = μ_no_fumador).
- Hipótesis Alternativa (H₁): La propina promedio es diferente para fumadores y no fumadores (μ_fumador ≠ μ_no_fumador).
import seaborn as sns
from scipy import stats
import matplotlib.pyplot as plt
# Cargar el dataset de propinas
tips = sns.load_dataset("tips")
print("Primeras 5 filas del dataset tips:")
print(tips.head())
# Separar las propinas por grupo (fumadores vs. no fumadores)
fumadores = tips[tips['smoker'] == 'Yes']['tip']
no_fumadores = tips[tips['smoker'] == 'No']['tip']
print(f"\nMedia de propina para fumadores: {fumadores.mean():.2f}")
print(f"Media de propina para no fumadores: {no_fumadores.mean():.2f}")
# Realizar la prueba t para dos muestras independientes (prueba de Welch, asumiendo varianzas desiguales)
# Usamos equal_var=False porque no asumimos que las varianzas de las propinas sean iguales entre grupos.
# Esto es una buena práctica a menos que haya una razón fuerte para asumir igualdad de varianzas.
t_stat, p_val = stats.ttest_ind(fumadores, no_fumadores, equal_var=False)
print("\n--- Prueba t (fumadores vs no fumadores) ---")
print(f" Estadístico t: {t_stat:.3f}")
print(f" Valor p: {p_val:.4f}")
alfa = 0.05
if p_val < alfa:
print(f" Dado que p-value ({p_val:.4f}) < alfa ({alfa}), se rechaza la hipótesis nula.")
print(" Conclusión: Hay una diferencia significativa en la propina promedio entre fumadores y no fumadores.")
else:
print(f" Dado que p-value ({p_val:.4f}) >= alfa ({alfa}), no se rechaza la hipótesis nula.")
print(" Conclusión: No hay evidencia suficiente de diferencia en la propina promedio entre fumadores y no fumadores.")
# Visualización de los resultados
plt.figure(figsize=(8, 6))
# Se corrige el llamado a boxplot para evitar el FutureWarning, asignando 'x' a 'hue' y ocultando la leyenda.
sns.boxplot(x='smoker', y='tip', data=tips, hue='smoker', palette={'Yes': 'lightcoral', 'No': 'skyblue'}, legend=False)
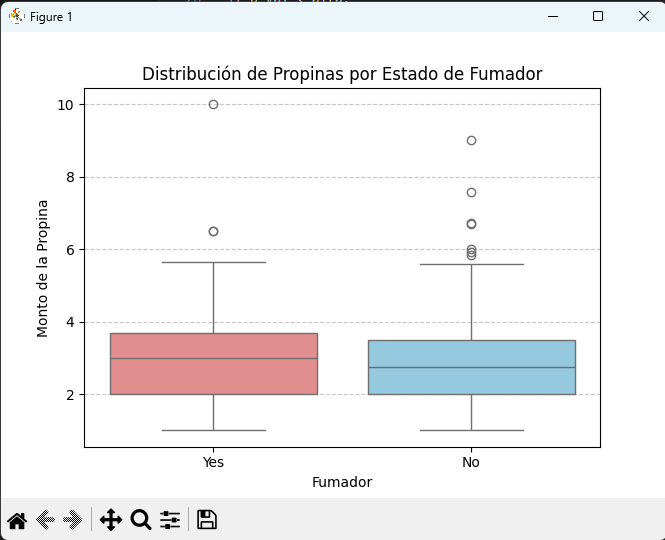
plt.title('Distribución de Propinas por Estado de Fumador')
plt.xlabel('Fumador')
plt.ylabel('Monto de la Propina')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
Resultado de la Ejecución
Primeras 5 filas del dataset tips:
total_bill tip sex smoker day time size
0 16.99 1.01 Female No Sun Dinner 2
1 10.34 1.66 Male No Sun Dinner 3
2 21.01 3.50 Male No Sun Dinner 3
3 23.68 3.31 Male No Sun Dinner 2
4 24.59 3.61 Female No Sun Dinner 4
Media de propina para fumadores: 3.01
Media de propina para no fumadores: 2.99
--- Prueba t (fumadores vs no fumadores) ---
Estadístico t: 0.092
Valor p: 0.9269
Dado que p-value (0.9269) >= alfa (0.05), no se rechaza la hipótesis nula.
Conclusión: No hay evidencia suficiente de diferencia en la propina promedio entre fumadores y no fumadores.
El resultado del p-value (0.9269) es muy alto, lo que indica que la pequeña diferencia observada en las medias de las propinas es muy probablemente producto del azar y no de una diferencia real entre los grupos.
10.2 Dataset titanic (supervivencia por categorías)
El dataset `titanic` contiene información sobre los pasajeros del Titanic, incluyendo si sobrevivieron, su clase, sexo, edad, etc. Es excelente para analizar la relación entre variables categóricas.
Pregunta de investigación: ¿Existe una asociación significativa entre el sexo del pasajero y la supervivencia?
- Hipótesis Nula (H₀): No hay asociación entre el sexo y la supervivencia (son independientes).
- Hipótesis Alternativa (H₁): Existe una asociación entre el sexo y la supervivencia (no son independientes).
import pandas as pd
import seaborn as sns
from scipy import stats
import matplotlib.pyplot as plt
# Cargar el dataset titanic
titanic = sns.load_dataset("titanic")
print("Primeras 5 filas del dataset titanic:")
print(titanic.head())
# Crear una tabla de contingencia (frecuencias cruzadas)
contingency_table = pd.crosstab(titanic['sex'], titanic['survived'])
print(f"\nTabla de Contingencia (Sexo vs Supervivencia):\n{contingency_table}")
# Realizar la prueba de Chi-cuadrado de independencia
chi2_stat, p_val, dof, expected = stats.chi2_contingency(contingency_table)
print("\n--- Prueba Chi-cuadrado (Sexo vs Supervivencia) ---")
print(f" Estadístico Chi-cuadrado: {chi2_stat:.3f}")
print(f" Valor p: {p_val:.4f}")
print(f" Grados de libertad (dof): {dof}")
print(f" Frecuencias esperadas:\n{expected.round(2)}")
alfa = 0.05
if p_val < alfa:
print(f" Dado que p-value ({p_val:.4f}) < alfa ({alfa}), se rechaza la hipótesis nula.")
print(" Conclusión: Existe una asociación significativa entre el sexo y la supervivencia en el Titanic.")
else:
print(f" Dado que p-value ({p_val:.4f}) >= alfa ({alfa}), no se rechaza la hipótesis nula.")
print(" Conclusión: No hay evidencia suficiente de asociación entre el sexo y la supervivencia en el Titanic.")
# Visualización de los resultados
plt.figure(figsize=(8, 6))
# Se corrige el diccionario de la paleta para usar llaves enteras (0 y 1) en lugar de strings.
sns.countplot(x='sex', hue='survived', data=titanic, palette={0: 'lightcoral', 1: 'skyblue'})
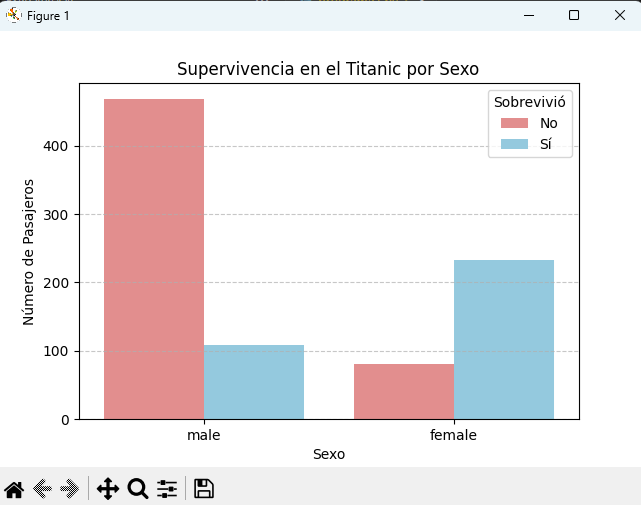
plt.title('Supervivencia en el Titanic por Sexo')
plt.xlabel('Sexo')
plt.ylabel('Número de Pasajeros')
plt.legend(title='Sobrevivió', labels=['No', 'Sí'])
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
Resultado de la Ejecución
Primeras 5 filas del dataset titanic:
survived pclass sex age sibsp parch fare embarked class who adult_male deck embark_town alive alone
0 0 3 male 22.0 1 0 7.2500 S Third man True NaN Southampton no False
1 1 1 female 38.0 1 0 71.2833 C First woman False C Cherbourg yes False
2 1 3 female 26.0 0 0 7.9250 S Third woman False NaN Southampton yes True
3 1 1 female 35.0 1 0 53.1000 S First woman False C Southampton yes False
4 0 3 male 35.0 0 0 8.0500 S Third man True NaN Southampton no True
Tabla de Contingencia (Sexo vs Supervivencia):
survived 0 1
sex
female 81 233
male 468 109
--- Prueba Chi-cuadrado (Sexo vs Supervivencia) ---
Estadístico Chi-cuadrado: 260.717
Valor p: 0.0000
Grados de libertad (dof): 1
Frecuencias esperadas:
[[193.47 120.53]
[355.53 221.47]]
Dado que p-value (0.0000) < alfa (0.05), se rechaza la hipótesis nula.
Conclusión: Existe una asociación significativa entre el sexo y la supervivencia en el Titanic.
El p-value extremadamente bajo (prácticamente cero) nos da una fuerte evidencia para rechazar la hipótesis nula. La conclusión es clara: el sexo y la supervivencia no son independientes. La visualización confirma esto, mostrando que la proporción de mujeres que sobrevivieron es drásticamente mayor que la de los hombres.
10.4 Presentación gráfica de resultados
Como se ha visto en los ejemplos anteriores, la visualización es una parte integral de la inferencia estadística. Los gráficos no solo ayudan a entender la distribución de los datos y las diferencias entre grupos, sino que también son cruciales para comunicar los hallazgos de manera efectiva.
- Box plots: Ideales para comparar la distribución de una variable numérica entre diferentes categorías.
- Histogramas y KDE plots: Muestran la forma de la distribución de una variable.
- Gráficos de barras (Count plots): Útiles para visualizar la frecuencia de categorías, especialmente en pruebas de Chi-cuadrado.
- Gráficos de dispersión: Pueden mostrar relaciones entre dos variables numéricas o cambios en mediciones pareadas.
Siempre acompaña tus análisis estadísticos con visualizaciones claras y bien etiquetadas para reforzar tus conclusiones y facilitar la comprensión.