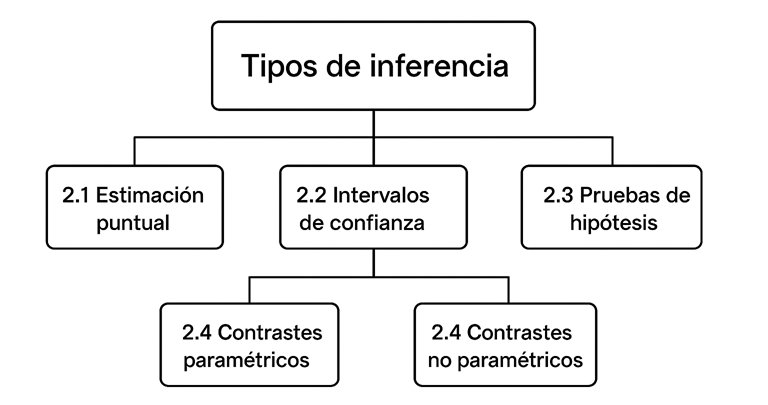
2. Tipos de inferencia

2.1 Estimación puntual

La estimación puntual consiste en utilizar un único valor, calculado a partir de los datos de una muestra, para estimar un parámetro desconocido de la población. Este valor único se conoce como estimador puntual.

• Ejemplo: Si queremos estimar la altura promedio de los estudiantes universitarios de un país, tomamos una muestra de 1000 estudiantes y calculamos su altura promedio. Este valor (ej., 1.70 metros) sería nuestra estimación puntual de la altura promedio de todos los estudiantes universitarios del país.
• Características: Los estimadores puntuales son fáciles de entender y comunicar. Sin embargo, por sí solos, no proporcionan información sobre la precisión de la estimación ni sobre la incertidumbre asociada. Es muy poco probable que la estimación puntual sea exactamente igual al verdadero parámetro poblacional.
• Estimadores comunes: La media muestral (x̄) es un estimador puntual de la media poblacional (μ), la proporción muestral (p̂) es un estimador puntual de la proporción poblacional (p), y la desviación estándar muestral (s) es un estimador puntual de la desviación estándar poblacional (σ).

2.2 Intervalos de confianza

A diferencia de la estimación puntual, que proporciona un único valor, un intervalo de confianza (IC) ofrece un rango de valores dentro del cual se espera que se encuentre el parámetro poblacional desconocido, con un cierto nivel de confianza. Es una forma más completa de estimación, ya que cuantifica la incertidumbre.

• Nivel de confianza: Se expresa como un porcentaje (ej., 90%, 95%, 99%) y representa la probabilidad de que el intervalo contenga el verdadero parámetro poblacional si el proceso de muestreo y cálculo se repitiera muchas veces.
• Ejemplo: Un intervalo de confianza del 95% para la altura promedio de los estudiantes universitarios podría ser [1.68 m, 1.72 m]. Esto significa que, si repitiéramos el muestreo y el cálculo del IC muchas veces, el 95% de esos intervalos contendrían la verdadera altura promedio de la población.
• Ventajas: Los IC son más informativos que las estimaciones puntuales porque no solo dan un valor estimado, sino también una medida de la precisión de esa estimación. Un intervalo más estrecho indica una estimación más precisa.
• Relación con las pruebas de hipótesis: Los IC pueden utilizarse para realizar pruebas de hipótesis. Si un valor hipotético (ej., el valor de la hipótesis nula) cae fuera del intervalo de confianza, se puede rechazar la hipótesis nula.

2.3 Pruebas de hipótesis

Las pruebas de hipótesis son un procedimiento formal para decidir si una afirmación (hipótesis) sobre una población es plausible o debe ser rechazada, basándose en la evidencia de una muestra. Este proceso implica formular dos hipótesis contrapuestas (nula y alternativa), recolectar datos, calcular un estadístico de prueba y un p-value, y luego tomar una decisión.

• Hipótesis Nula (H₀): Es la afirmación que se asume verdadera por defecto y que se intenta refutar. Generalmente postula que no hay efecto o diferencia.
• Hipótesis Alternativa (H₁): Es la afirmación que se intenta probar. Postula que sí hay un efecto o diferencia.
• Estadístico de prueba: Un valor calculado a partir de la muestra que se utiliza para evaluar la evidencia contra la hipótesis nula (ej., estadístico t, F, chi-cuadrado).
• P-value: La probabilidad de observar los datos de la muestra (o datos más extremos) si la hipótesis nula fuera verdadera. Un p-value pequeño (típicamente < 0.05) sugiere que los datos son inconsistentes con H₀, llevando a su rechazo.
• Ejemplo: Probar si un nuevo medicamento reduce la presión arterial.
  • Hipótesis Nula (H₀): El medicamento no tiene efecto sobre la presión arterial. Esta es la afirmación de "no cambio" o "no efecto". Si medimos la presión arterial promedio antes y después del tratamiento, no encontraremos una diferencia estadísticamente significativa.
  • Hipótesis Alternativa (H₁): El medicamento sí reduce la presión arterial. Esta es la afirmación que los investigadores quieren probar. Esperarían encontrar que la presión arterial promedio después de tomar el medicamento es significativamente menor que antes.

  El objetivo del estudio sería recolectar datos de pacientes para determinar si la evidencia es lo suficientemente fuerte como para rechazar la hipótesis nula en favor de la alternativa.

2.4 Contrastes paramétricos vs. no paramétricos

Las pruebas de hipótesis se dividen en dos grandes categorías según los supuestos que hacen sobre la distribución de los datos:

• Pruebas Paramétricas:

  Son pruebas estadísticas que hacen supuestos específicos sobre la distribución de la población de la que se extraen los datos. El supuesto más común es que los datos siguen una distribución normal. También suelen requerir que las varianzas de los grupos sean iguales (homocedasticidad) y que los datos sean de escala de intervalo o razón.

  Ejemplos comunes:

  • Prueba t de Student: Se utiliza para comparar las medias (promedios) de uno o dos grupos.
    • Para una muestra: Compara la media de un grupo con un valor conocido (ej: ¿la producción media de nuestra fábrica es de 500 unidades/día?).
    • Para dos muestras independientes: Compara las medias de dos grupos distintos (ej: ¿los estudiantes del grupo A tienen calificaciones promedio diferentes a los del grupo B?).
    • Para muestras pareadas: Compara las medias del mismo grupo en dos momentos diferentes (ej: ¿mejoró el rendimiento de los atletas después de un entrenamiento específico?).
  • ANOVA (Análisis de Varianza): Es como una extensión de la prueba t, pero permite comparar las medias de tres o más grupos a la vez (ej: ¿existe una diferencia en la eficacia de tres medicamentos distintos para el mismo tratamiento?).
  • Regresión Lineal: Se usa para modelar la relación entre dos o más variables, usualmente para predecir el valor de una variable basándose en el valor de otra (ej: ¿podemos predecir el precio de una casa basándonos en su tamaño en metros cuadrados?).

  Ventajas: Son más potentes (tienen mayor probabilidad de detectar un efecto real si existe) cuando sus supuestos se cumplen.

• Pruebas No Paramétricas:

  Son pruebas estadísticas que no hacen supuestos sobre la forma de la distribución de la población. Son más flexibles y robustas, lo que las hace adecuadas para datos que no cumplen los supuestos de las pruebas paramétricas, o para datos ordinales o nominales.

  Ejemplos comunes:

  • Prueba U de Mann-Whitney: Es la alternativa no paramétrica a la prueba t para muestras independientes. Se usa para comparar dos grupos y determinar si uno tiende a tener valores más altos que el otro, sin asumir una distribución normal de los datos (ej: ¿los pacientes del grupo A reportan un nivel de satisfacción mayor que los del grupo B, donde la satisfacción se mide en una escala ordinal?).
  • Prueba de los rangos con signo de Wilcoxon: Es la alternativa no paramétrica a la prueba t para muestras pareadas. Se utiliza para comparar dos mediciones del mismo grupo en momentos diferentes (un "antes y después") cuando no se puede suponer normalidad (ej: ¿cambió significativamente el ranking de preferencias de un grupo de consumidores después de ver un anuncio?).
  • Prueba de Chi-cuadrado (χ²): Se utiliza para trabajar con datos categóricos. Su aplicación más común es determinar si existe una asociación o relación entre dos variables categóricas (ej: ¿existe una asociación entre el género de una persona y su preferencia por un partido político?). Compara las frecuencias que observas en tu muestra con las frecuencias que esperarías si las variables fueran independientes.

  Ventajas: Son más robustas frente a violaciones de supuestos y pueden usarse con una gama más amplia de tipos de datos.

  Desventajas: Generalmente son menos potentes que las pruebas paramétricas cuando los supuestos de estas últimas se cumplen.

La elección entre una prueba paramétrica y no paramétrica depende de la naturaleza de los datos y de si se cumplen los supuestos necesarios.

2.5 Aplicaciones en distintos contextos

La inferencia estadística es una herramienta transversal con aplicaciones en casi todos los campos de estudio y la industria:

• Medicina y Farmacología:

  Ensayos clínicos para determinar la eficacia y seguridad de nuevos fármacos o tratamientos. Comparación de tasas de curación, efectos secundarios, etc.

• Marketing y Negocios:

  Pruebas A/B para optimizar sitios web, campañas publicitarias o características de productos. Análisis de la efectividad de diferentes estrategias de precios o promociones.

• Ciencias Sociales y Psicología:

  Análisis de encuestas de opinión, estudios de comportamiento humano, evaluación de programas educativos o intervenciones sociales.

• Ingeniería y Control de Calidad:

  Monitoreo de procesos de fabricación para asegurar que los productos cumplen con las especificaciones. Detección de defectos y optimización de la producción.

• Finanzas y Economía:

  Modelado de riesgos, predicción de tendencias del mercado, evaluación de políticas económicas y análisis de inversiones.

• Ciencia de Datos e Inteligencia Artificial:

  Validación de modelos predictivos, selección de características (feature selection), cuantificación de la incertidumbre en las predicciones y evaluación de la significancia de los resultados de algoritmos.

En cada uno de estos campos, la inferencia estadística proporciona el marco para tomar decisiones basadas en datos de manera rigurosa y con una comprensión clara de la incertidumbre.