6. Distribuciones estadísticas de referencia

6.1 ¿Por qué necesitamos estas distribuciones?

En la inferencia estadística, no podemos simplemente decir que la media de nuestra muestra es "diferente" a un valor hipotético. Necesitamos saber si es significativamente diferente. Pero, ¿cómo medimos la "significancia"?

Aquí es donde entran las distribuciones de referencia. Piensa en ellas como mapas teóricos o reglas estandarizadas. Cuando realizamos una prueba, calculamos un "estadístico de prueba" (como un valor t o un valor χ²). Luego, comparamos nuestro estadístico con su distribución de referencia correspondiente para responder a la pregunta clave:

"Si la hipótesis nula fuera cierta (es decir, si no hubiera un efecto real), ¿cuán probable sería obtener un estadístico de prueba como el que hemos obtenido, o incluso más extremo?"

Estas distribuciones nos dan la probabilidad (el p-value) y nos permiten tomar una decisión informada. En este tema, exploraremos las cuatro distribuciones más fundamentales que forman la base de la mayoría de las pruebas de hipótesis.

6.2 Distribución Normal: La Piedra Angular

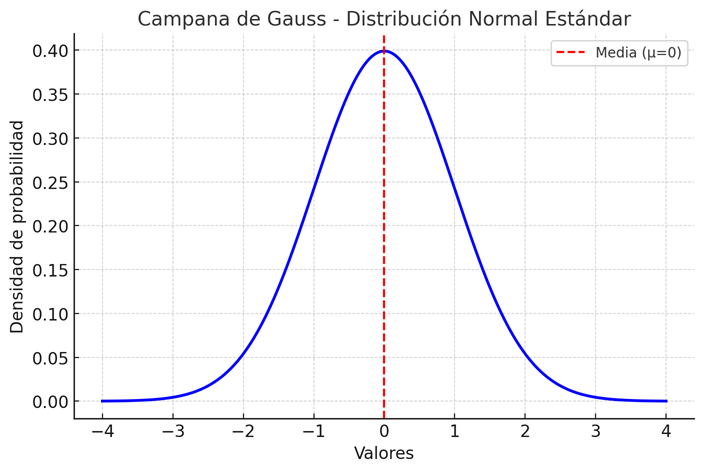
La distribución normal, o "campana de Gauss", es la reina de las distribuciones. Su fama se debe principalmente a un concepto casi mágico llamado Teorema del Límite Central (TLC).

El Teorema del Límite Central (TLC) en Acción

El TLC establece algo asombroso: si tomas muchas muestras de cualquier población (incluso una con una distribución extraña) y calculas la media de cada una de esas muestras, la distribución de esas medias muestrales tenderá a formar una curva normal perfecta.

Analogía: Imagina que mides la altura de miles de personas en un festival de disfraces. La distribución de alturas podría ser muy rara (con grupos de gente alta, gente baja, etc.). Ahora, si tomas grupos de 30 personas al azar, calculas su altura promedio, y repites esto cientos de veces, la gráfica de todos esos promedios que has calculado se verá como una campana de Gauss.

Esta es la razón por la que podemos usar la distribución normal para hacer inferencias sobre las medias muestrales, incluso si no sabemos cómo se distribuye la población original.

Características Clave:

• Simétrica: La media, la mediana y la moda coinciden en el centro.
• Definida por dos parámetros: La media (μ), que la centra, y la desviación estándar (σ), que determina cuán ancha o estrecha es la campana.
• Base para pruebas paramétricas: Muchas pruebas (como la prueba Z y partes de la prueba t) asumen que los datos o los errores siguen una distribución normal.

6.3 Distribución t de Student: La Versión Cautelosa de la Normal

La distribución t es una pariente cercana de la distribución normal. Podríamos pensar en ella como una versión más cautelosa o escéptica de la campana de Gauss.

¿Por qué y cuándo la usamos?

La usamos en el escenario más común de la estadística: cuando trabajamos con una muestra, no conocemos la desviación estándar de toda la población (σ), y por lo tanto tenemos que estimarla usando la desviación estándar de nuestra muestra (s).

Esta estimación introduce una capa extra de incertidumbre. La distribución t se ajusta a esta incertidumbre, especialmente cuando nuestras muestras son pequeñas.

Colas Pesadas y Grados de Libertad

• Colas "Pesadas": La distribución t tiene más área en sus colas en comparación con la normal. Esto significa que considera que los valores extremos son un poco más probables. En la práctica, esto implica que la distribución t exige evidencia más fuerte (un estadístico t más grande) para rechazar la hipótesis nula. Es más difícil de convencer.
• Grados de Libertad (df): Es el único parámetro que define la forma de la distribución t, y está directamente relacionado con el tamaño de la muestra (df = n - 1).
  • Con pocos grados de libertad (muestras pequeñas), la distribución t es ancha y plana, reflejando mucha incertidumbre.
  • A medida que los grados de libertad aumentan (muestras más grandes), la distribución t se vuelve más y más parecida a la distribución normal. Con una muestra lo suficientemente grande, son prácticamente idénticas.

Aplicación principal: Es la base para las pruebas t y los intervalos de confianza para medias, que son de las herramientas más usadas en la estadística.

6.4 Distribución Chi-cuadrado (χ²): La Prueba de las Diferencias

La distribución Chi-cuadrado (o Ji-cuadrado) es nuestra herramienta para trabajar con datos categóricos (datos que se cuentan en categorías, como "Sí/No/Quizás" o "Rojo/Verde/Azul"). Su propósito principal es evaluar cuán bien nuestros datos observados se ajustan a un modelo o teoría que teníamos.

El estadístico χ² es, en esencia, una medida de la distancia total entre lo que observamos y lo que esperábamos observar. Siempre es un valor positivo; un valor de 0 significa un ajuste perfecto, y valores más grandes indican una mayor discrepancia.

Aplicaciones Principales con Analogías

• Prueba de Bondad de Ajuste: Responde a la pregunta: "¿Los datos que recolecté siguen la distribución que yo esperaba?"

  Analogía: Un fabricante de M&M's afirma que el 20% de los caramelos son rojos, 20% azules, 20% verdes, 20% amarillos y 20% marrones. Tú compras una bolsa grande, cuentas los colores y comparas tus conteos observados con los conteos que esperarías según la afirmación del fabricante. El estadístico χ² te dice si la diferencia es tan grande que deberías dudar de la afirmación del fabricante.

• Prueba de Independencia: Responde a la pregunta: "¿Están estas dos variables categóricas relacionadas o son independientes?"

  Analogía: Quieres saber si la preferencia por un género de película (Comedia, Acción, Drama) está relacionada con el género de la persona (Hombre, Mujer). Creas una tabla de contingencia con tus datos. La prueba χ² compara tus conteos observados con los que esperarías si no hubiera ninguna relación entre las variables. Un valor χ² alto sugiere que sí hay una asociación: el género de la persona influye en su preferencia por un tipo de película.

Al igual que otras distribuciones, su forma depende de los grados de libertad (df), que en este contexto se relacionan con el número de categorías que se están comparando.

6.5 Distribución F: La Comparadora de Varianzas (ANOVA)

La distribución F es la base del Análisis de Varianza (ANOVA), una técnica poderosa para comparar las medias de tres o más grupos simultáneamente.

Mientras que una prueba t puede comparar dos medias, usar múltiples pruebas t para comparar muchos grupos aumenta drásticamente la probabilidad de cometer un error (un falso positivo). ANOVA, usando la distribución F, resuelve este problema.

La Lógica de ANOVA y el Estadístico F

El estadístico F se puede entender de forma intuitiva como una simple razón:

• Variabilidad ENTRE grupos: Mide cuán apartadas están las medias de cada grupo entre sí. Si las medias de los grupos están muy dispersas, este valor es grande.
• Variabilidad DENTRO de los grupos: Mide cuán dispersos están los datos dentro de cada grupo individual. Es una medida del "ruido" o variabilidad natural de los datos.

Analogía: Imagina que estás probando tres fertilizantes diferentes (A, B, C) en tres grupos de plantas. Después de un mes, mides sus alturas.

• Si el estadístico F es grande, significa que la variabilidad ENTRE los promedios de altura de los grupos A, B y C es mucho mayor que la variabilidad natural DENTRO de cada grupo. Esto sugiere que los fertilizantes tienen efectos realmente diferentes.
• Si el estadístico F es pequeño (cercano a 1), significa que la diferencia entre las medias de los grupos es similar al "ruido" dentro de ellos, por lo que no podemos concluir que haya una diferencia real entre los fertilizantes.

La distribución F, definida por dos tipos de grados de libertad (uno para los grupos y otro para los datos totales), nos dice si nuestro estadístico F es lo suficientemente grande como para ser estadísticamente significativo.

6.6 Visualización de las Distribuciones en Python

Una de las mejores maneras de entender estas distribuciones es verlas en acción. El siguiente código en Python utiliza las librerías NumPy para generar datos aleatorios, SciPy para acceder a las funciones de las distribuciones y Matplotlib para visualizarlas.

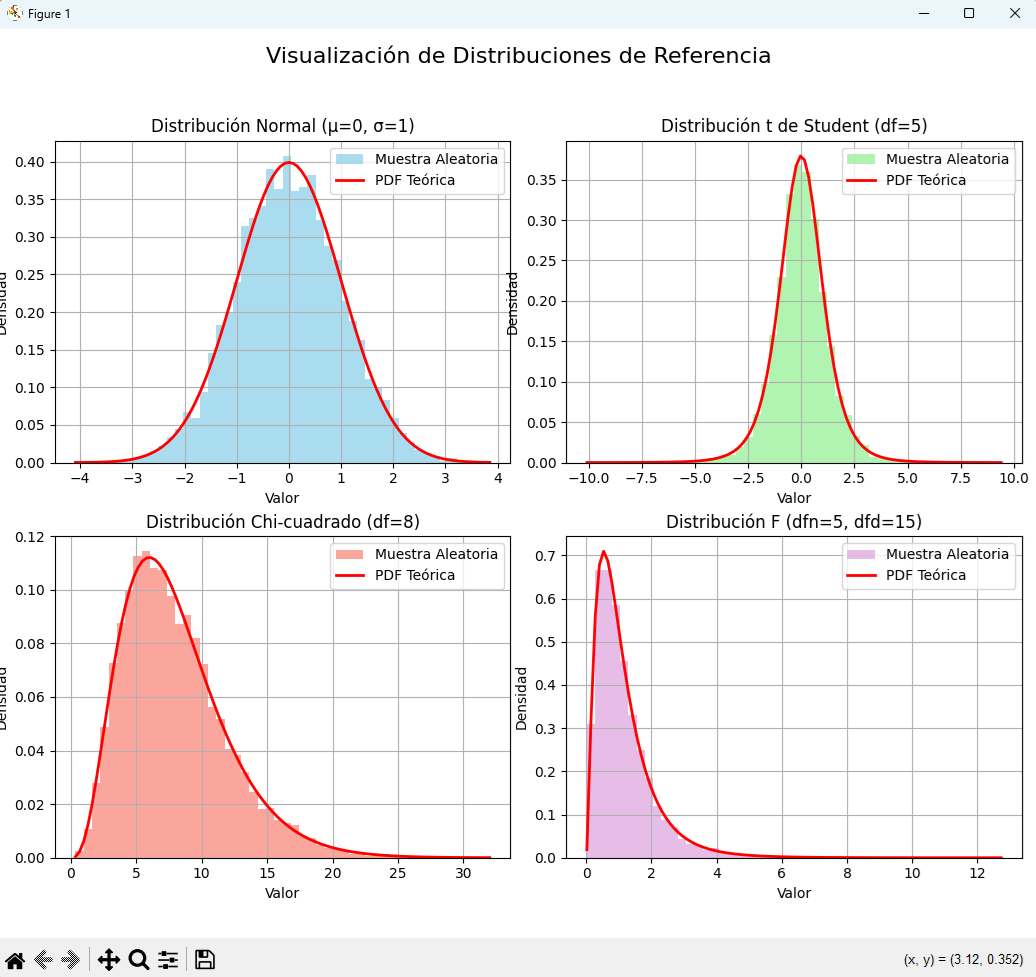
El script creará un panel con cuatro gráficos, uno para cada distribución, permitiéndonos comparar sus formas características.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, chi2, f, norm

# --- 1. Configuración General del Gráfico ---
# Crear una figura grande que contendrá 4 sub-gráficos (2 filas, 2 columnas)
plt.figure(figsize=(14, 10))
# Título general para toda la figura
plt.suptitle('Visualización de Distribuciones de Referencia', fontsize=16)

# --- 2. Distribución Normal ---
mu, sigma = 0, 1 # Media y desviación estándar para la normal estándar
s_normal = np.random.normal(mu, sigma, 10000) # Generar 10000 puntos aleatorios

# Seleccionar el primer sub-gráfico
plt.subplot(2, 2, 1)
# Crear un histograma de los datos. density=True normaliza el área a 1.
plt.hist(s_normal, bins=50, density=True, alpha=0.7, color='skyblue', label='Muestra Aleatoria')
# Dibujar la línea teórica (PDF - Función de Densidad de Probabilidad)
x = np.linspace(s_normal.min(), s_normal.max(), 100)
plt.plot(x, norm.pdf(x, mu, sigma), 'r-', lw=2, label='PDF Teórica')
plt.title('Distribución Normal (μ=0, σ=1)')
plt.xlabel('Valor')
plt.ylabel('Densidad')
plt.legend()
plt.grid(True)

# --- 3. Distribución t de Student ---
df_t = 5 # Grados de libertad (un valor bajo para notar las colas pesadas)
s_t = t.rvs(df_t, size=10000)

# Seleccionar el segundo sub-gráfico
plt.subplot(2, 2, 2)
plt.hist(s_t, bins=50, density=True, alpha=0.7, color='lightgreen', label='Muestra Aleatoria')
# Dibujar la PDF teórica de la t-distribución
x = np.linspace(s_t.min(), s_t.max(), 100)
plt.plot(x, t.pdf(x, df_t), 'r-', lw=2, label='PDF Teórica')
plt.title(f'Distribución t de Student (df={df_t})')
plt.xlabel('Valor')
plt.ylabel('Densidad')
plt.legend()
plt.grid(True)

# --- 4. Distribución Chi-cuadrado ---
df_chi2 = 8 # Grados de libertad
s_chi2 = chi2.rvs(df_chi2, size=10000)

# Seleccionar el tercer sub-gráfico
plt.subplot(2, 2, 3)
plt.hist(s_chi2, bins=50, density=True, alpha=0.7, color='salmon', label='Muestra Aleatoria')
# Dibujar la PDF teórica
x = np.linspace(s_chi2.min(), s_chi2.max(), 100)
plt.plot(x, chi2.pdf(x, df_chi2), 'r-', lw=2, label='PDF Teórica')
plt.title(f'Distribución Chi-cuadrado (df={df_chi2})')
plt.xlabel('Valor')
plt.ylabel('Densidad')
plt.legend()
plt.grid(True)

# --- 5. Distribución F ---
dfn, dfd = 5, 15 # Grados de libertad del numerador y denominador
s_f = f.rvs(dfn, dfd, size=10000)

# Seleccionar el cuarto sub-gráfico
plt.subplot(2, 2, 4)
plt.hist(s_f, bins=50, density=True, alpha=0.7, color='plum', label='Muestra Aleatoria')
# Dibujar la PDF teórica
x = np.linspace(s_f.min(), s_f.max(), 100)
plt.plot(x, f.pdf(x, dfn, dfd), 'r-', lw=2, label='PDF Teórica')
plt.title(f'Distribución F (dfn={dfn}, dfd={dfd})')
plt.xlabel('Valor')
plt.ylabel('Densidad')
plt.legend()
plt.grid(True)

# Ajustar el diseño para que los títulos y etiquetas no se superpongan
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
# Mostrar el gráfico
plt.show()
            

Análisis de los Gráficos

Al ejecutar este código, podrás observar:

• Normal: La perfecta y simétrica campana de Gauss.
• t de Student: Se parece mucho a la normal, pero si la comparas con una normal estándar, notarás que es un poco más baja en el pico y más ancha en las colas, reflejando su naturaleza "cautelosa".
• Chi-cuadrado y F: Ambas son distribuciones asimétricas y solo toman valores positivos. Sus formas cambian drásticamente según sus grados de libertad.

Estos gráficos demuestran cómo una muestra aleatoria grande (el histograma) tiende a seguir la forma de su distribución teórica subyacente (la línea roja).