8. Pruebas t para dos muestras

8.1 Concepto y cuándo usarla

Las pruebas t para dos muestras independientes se utilizan para determinar si existe una diferencia estadísticamente significativa entre las medias de dos grupos no relacionados. Es decir, los individuos de un grupo no tienen ninguna relación con los individuos del otro grupo.

Situaciones comunes:

• Comparar el rendimiento de dos grupos de estudiantes que recibieron diferentes métodos de enseñanza.
• Evaluar si un nuevo medicamento tiene un efecto diferente en dos grupos de pacientes (uno con placebo, otro con el medicamento).
• Analizar si los salarios promedio difieren entre hombres y mujeres en una industria específica.

Al igual que la prueba t para una muestra, asume que los datos de cada grupo provienen de poblaciones con distribución aproximadamente normal y que la desviación estándar de la población es desconocida.

8.2 Independientes con varianzas iguales (Student's t-test)

Esta versión de la prueba t asume que las varianzas de las poblaciones de las que provienen las dos muestras son iguales (homocedasticidad). Si esta suposición se cumple, se utiliza una estimación combinada de la varianza para calcular el error estándar.

Hipótesis:

• H₀: μ₁ = μ₂ (Las medias de las dos poblaciones son iguales)
• H₁: μ₁ ≠ μ₂ (Las medias de las dos poblaciones son diferentes)

Antes de aplicar esta prueba, es recomendable realizar una prueba de igualdad de varianzas (como la prueba de Levene o la prueba F) para verificar el supuesto de homocedasticidad.

8.3 Independientes con varianzas distintas (Welch's t-test)

La prueba t de Welch es una adaptación de la prueba t para dos muestras independientes que no asume que las varianzas de las poblaciones son iguales (heterocedasticidad). Es más robusta y se recomienda su uso cuando no se está seguro de la igualdad de varianzas o cuando las pruebas de varianza sugieren que son diferentes.

Hipótesis: Las mismas que para la prueba t de Student (H₀: μ₁ = μ₂, H₁: μ₁ ≠ μ₂).

La prueba de Welch ajusta los grados de libertad para compensar la posible desigualdad de varianzas, lo que la hace más conservadora y menos propensa a cometer un Error Tipo I cuando las varianzas son realmente diferentes.

8.4 Ejemplo aplicado en Python (ttest_ind)

Utilizaremos scipy.stats.ttest_ind para comparar las puntuaciones de dos grupos de estudiantes que recibieron diferentes métodos de estudio.

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns

# Puntuaciones del Grupo A (método de estudio tradicional)
grupo_a = np.array([85, 88, 90, 82, 87, 84, 89, 86, 83, 91, 79, 85, 88, 80, 86])

# Puntuaciones del Grupo B (nuevo método de estudio)
grupo_b = np.array([78, 80, 83, 79, 81, 77, 82, 80, 76, 84, 75, 81, 79, 83, 78])

# Nivel de significancia
alfa = 0.05

print(f"Media Grupo A: {np.mean(grupo_a):.2f}, Desv. Est. Grupo A: {np.std(grupo_a, ddof=1):.2f}")
print(f"Media Grupo B: {np.mean(grupo_b):.2f}, Desv. Est. Grupo B: {np.std(grupo_b, ddof=1):.2f}")

# --- Prueba t asumiendo varianzas iguales (Student's t-test) ---
# equal_var=True es el valor por defecto, pero se especifica para claridad
t_statistic_eq, p_value_eq = stats.ttest_ind(grupo_a, grupo_b, equal_var=True)

print("\n--- Prueba t (asumiendo varianzas iguales) ---")
print(f"Estadístico t: {t_statistic_eq:.3f}")
print(f"Valor p: {p_value_eq:.4f}")

if p_value_eq < alfa:
    print("Decisión: Se rechaza la hipótesis nula.")
    print("Conclusión: Hay una diferencia significativa entre las medias de los grupos (asumiendo varianzas iguales).")
else:
    print("Decisión: No se rechaza la hipótesis nula.")
    print("Conclusión: No hay evidencia suficiente de diferencia entre las medias (asumiendo varianzas iguales).")

# --- Prueba t de Welch (asumiendo varianzas desiguales) ---
# equal_var=False para la prueba de Welch
t_statistic_welch, p_value_welch = stats.ttest_ind(grupo_a, grupo_b, equal_var=False)

print("\n--- Prueba t de Welch (asumiendo varianzas desiguales) ---")
print(f"Estadístico t: {t_statistic_welch:.3f}")
print(f"Valor p: {p_value_welch:.4f}")

if p_value_welch < alfa:
    print("Decisión: Se rechaza la hipótesis nula.")
    print("Conclusión: Hay una diferencia significativa entre las medias de los grupos (asumiendo varianzas desiguales).")
else:
    print("Decisión: No se rechaza la hipótesis nula.")
    print("Conclusión: No hay evidencia suficiente de diferencia entre las medias (asumiendo varianzas desiguales).")
            

En este ejemplo, se realizan ambas pruebas. La elección de cuál interpretar dependerá de si se cumple o no el supuesto de igualdad de varianzas.

8.5 Visualización de resultados

La visualización es clave para entender las diferencias entre los grupos y complementar la interpretación de las pruebas estadísticas. Los box plots son una excelente opción para comparar distribuciones.

# Visualización de los datos con Box Plot
plt.figure(figsize=(8, 6))
sns.boxplot(data=[grupo_a, grupo_b], palette=['skyblue', 'lightcoral'])
plt.xticks([0, 1], ['Grupo A', 'Grupo B'])
plt.title('Comparación de Puntuaciones entre Grupo A y Grupo B')
plt.ylabel('Puntuación')
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()

# También se pueden usar histogramas para ver la forma de la distribución
plt.figure(figsize=(10, 5))
sns.histplot(grupo_a, color='skyblue', kde=True, label='Grupo A', stat='density')
sns.histplot(grupo_b, color='lightcoral', kde=True, label='Grupo B', stat='density')
plt.title('Histograma de Puntuaciones por Grupo')
plt.xlabel('Puntuación')
plt.ylabel('Densidad')
plt.legend()
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
            

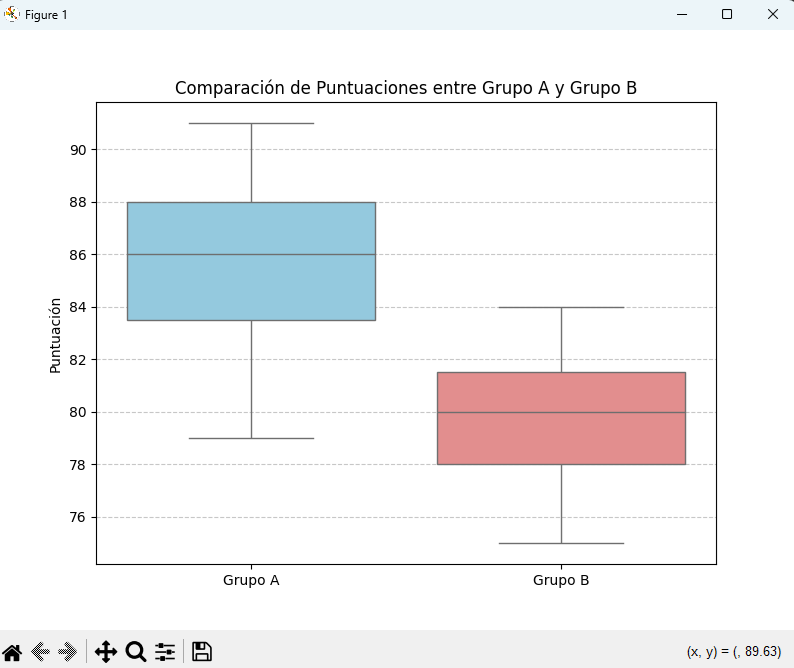
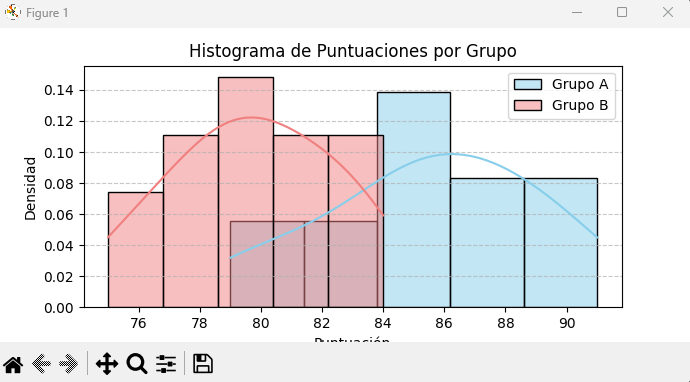
Los gráficos nos permiten ver la superposición de las distribuciones, las medianas, los rangos intercuartílicos y la presencia de valores atípicos, lo que enriquece la interpretación de los p-values.

8.6 Interpretación en problemas reales

En un contexto real, la interpretación de estas pruebas t nos permite tomar decisiones informadas:

• Si la prueba es significativa, podemos concluir que el nuevo método de estudio (Grupo B) realmente produce un cambio en las puntuaciones promedio en comparación con el método tradicional (Grupo A).
• Si no es significativa, no tenemos evidencia suficiente para afirmar que el nuevo método es mejor (o peor), y podríamos necesitar más investigación, un tamaño de muestra mayor o un diseño experimental diferente.

Es fundamental no solo reportar el p-value, sino también la magnitud de la diferencia (tamaño del efecto) y el contexto práctico de los resultados.