9. Pruebas t pareadas
9.1 Concepto y aplicaciones típicas (antes vs. después)
La prueba t pareada (o t de muestras relacionadas) se utiliza cuando se tienen dos conjuntos de observaciones que están relacionadas o "pareadas". Esto significa que cada observación en un grupo tiene una correspondencia directa con una observación en el otro grupo. El objetivo es determinar si existe una diferencia estadísticamente significativa entre las medias de estas dos mediciones relacionadas.
Aplicaciones típicas:
- Diseños "antes y después": Medir una variable en los mismos sujetos antes y después de una intervención, tratamiento o evento (ej., peso antes y después de una dieta, presión arterial antes y después de un fármaco).
- Comparación de dos tratamientos en los mismos sujetos: Cada sujeto recibe ambos tratamientos en diferentes momentos, o se aplica un tratamiento a un ojo y otro tratamiento al otro ojo del mismo paciente.
- Estudios de gemelos: Comparar características entre gemelos idénticos para controlar factores genéticos.
La clave es que las dos muestras no son independientes; las mediciones están vinculadas por el mismo individuo o unidad experimental.
9.2 Fórmulas y cálculo manual
La prueba t pareada se basa en las diferencias entre cada par de observaciones. En lugar de comparar directamente las medias de los dos grupos, se calcula la diferencia para cada par y luego se realiza una prueba t de una muestra sobre estas diferencias.
Pasos:
- Calcular la diferencia (d) para cada par de observaciones (d = X₂ - X₁).
- Calcular la media de estas diferencias (d̄).
- Calcular la desviación estándar de las diferencias (s_d).
- Calcular el estadístico t utilizando la fórmula:
t = d̄ / (s_d / √n)
Donde:
d̄es la media de las diferencias.s_des la desviación estándar de las diferencias.nes el número de pares de observaciones.
Los grados de libertad para esta prueba son n-1.
Hipótesis:
- H₀: μ_d = 0 (La media de las diferencias es cero; no hay cambio o efecto).
- H₁: μ_d ≠ 0 (La media de las diferencias no es cero; hay un cambio o efecto).
9.3 Ejemplo en Python (ttest_rel)
Vamos a evaluar la efectividad de un programa de entrenamiento físico. Medimos el tiempo (en segundos) que un grupo de atletas tarda en correr 100 metros antes y después de un programa de 8 semanas.
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
# Tiempos de los atletas antes del programa (en segundos)
tiempo_antes = np.array([12.5, 13.1, 12.0, 13.5, 12.8, 13.0, 12.7, 13.2, 12.9, 13.3])
# Tiempos de los mismos atletas después del programa (en segundos)
tiempo_despues = np.array([12.0, 12.8, 11.5, 13.0, 12.5, 12.6, 12.2, 12.9, 12.4, 12.8])
# Nivel de significancia
alfa = 0.05
print(f"Tiempos antes: {tiempo_antes}")
print(f"Tiempos después: {tiempo_despues}")
print(f"Media antes: {np.mean(tiempo_antes):.2f}")
print(f"Media después: {np.mean(tiempo_despues):.2f}")
# Realizar la prueba t pareada
# stats.ttest_rel devuelve el estadístico t y el p-value
t_statistic, p_value = stats.ttest_rel(tiempo_antes, tiempo_despues)
print(f"\nEstadístico t: {t_statistic:.3f}")
print(f"Valor p: {p_value:.4f}")
print(f"Nivel de significancia (alfa): {alfa}")
# Interpretación de resultados
if p_value < alfa:
print("\nDecisión: Se rechaza la hipótesis nula.")
print("Conclusión: Hay evidencia estadística significativa para afirmar que el programa de entrenamiento tuvo un efecto en el tiempo de carrera.")
else:
print("\nDecisión: No se rechaza la hipótesis nula.")
print("Conclusión: No hay evidencia estadística suficiente para afirmar que el programa de entrenamiento tuvo un efecto en el tiempo de carrera.")
En este caso, un p-value bajo indicaría que la reducción promedio en los tiempos de carrera no es atribuible al azar, sino al efecto del programa.
9.4 Caso aplicado con dataset real
Aunque el ejemplo anterior usa datos simulados, en un caso real se podría cargar un dataset que contenga mediciones pareadas. Por ejemplo, un dataset de pacientes con mediciones de presión arterial antes y después de un tratamiento. La lógica de aplicación de ttest_rel sería idéntica.
Consideraciones para datos reales:
- Asegurarse de que los datos estén correctamente emparejados (es decir, que la primera medición de un sujeto corresponda a la segunda medición del mismo sujeto).
- Manejar valores faltantes de manera apropiada, ya que la prueba t pareada requiere pares completos de observaciones.
9.5 Visualización e interpretación
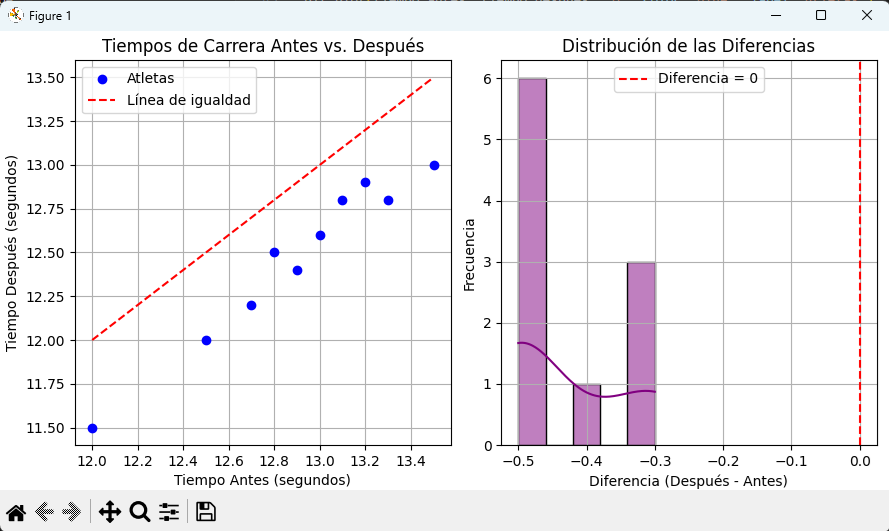
Para visualizar los resultados de una prueba t pareada, un gráfico de dispersión con una línea que une los puntos de "antes" y "después" para cada sujeto es muy informativo. También se puede graficar la distribución de las diferencias.
# Calcular las diferencias
diferencias = tiempo_despues - tiempo_antes
plt.figure(figsize=(10, 6))
# Gráfico de dispersión con líneas conectando los puntos (antes vs despues)
plt.subplot(1, 2, 1) # 1 fila, 2 columnas, primer gráfico
plt.plot(tiempo_antes, tiempo_despues, 'o', color='blue', label='Atletas')
plt.plot([min(tiempo_antes), max(tiempo_antes)], [min(tiempo_antes), max(tiempo_antes)], '--r', label='Línea de igualdad')
plt.xlabel('Tiempo Antes (segundos)')
plt.ylabel('Tiempo Después (segundos)')
plt.title('Tiempos de Carrera Antes vs. Después')
plt.legend()
plt.grid(True)
# Histograma de las diferencias
plt.subplot(1, 2, 2) # Segundo gráfico
sns.histplot(diferencias, kde=True, color='purple')
plt.axvline(0, color='red', linestyle='--', label='Diferencia = 0')
plt.xlabel('Diferencia (Después - Antes)')
plt.ylabel('Frecuencia')
plt.title('Distribución de las Diferencias')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
Interpretación:
- Si la mayoría de los puntos en el gráfico de dispersión caen por debajo de la línea de igualdad (y=x), indica que los tiempos "después" son menores que los tiempos "antes".
- Si el histograma de las diferencias está centrado significativamente lejos de cero, sugiere un efecto real.
- Un p-value bajo, junto con una visualización que muestre una tendencia clara, refuerza la conclusión de que la intervención tuvo un efecto significativo.