17 - Vectores estáticos: ordenamiento
El ordenamiento de un vector se logra intercambiando las componentes de manera que:
Vec[1] <= Vec[2] <= Vec[3] etc.
El contenido de la componente Vec[1] sea menor o igual al contenido de la componente Vec[2] y así sucesivamente.
Si se cumple lo dicho anteriormente decimos que el vector está ordenado de menor a mayor. Igualmente podemos ordenar un vector de mayor a menor.
Se puede ordenar tanto vectores con componentes de tipo Integer, Double como String. En este último caso el ordenamiento es alfabético.
Algoritmo para el ordenamiento de un vector.
Problema 1
Ordenar el vector Sueldos de menor a mayor.

Para dejar el mayor en la última posición del vector:
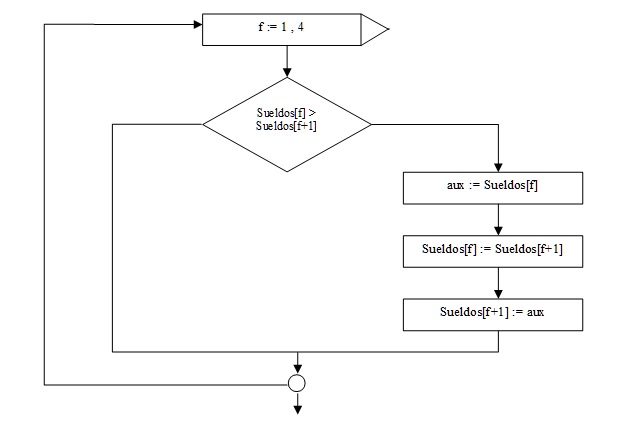
Esta primera aproximación tiene por objetivo analizar los intercambios de elementos dentro del vector.
El algoritmo consiste en comparar si la primera componente es mayor a la segunda, en caso que la condición sea verdadera, intercambiamos los contenidos de las componentes.
En este ejemplo: ¿es 1200 mayor a 750? La respuesta es verdadera, por lo tanto intercambiamos el contenido de la componente 1 con el de la componente 2.
Luego comparamos el contenido de la componente 2 con el de la componente 3: ¿Es 1200 mayor a 820? La respuesta es verdadera entonces intercambiamos.
Si hay 5 componentes hay que hacer 4 comparaciones, por eso el for es de 1 a 4. Generalizando: si el vector tiene N componentes hay que hacer N-1 comparaciones.
Cuando f = 1 f = 2 f = 3 f = 4 750 750 750 750 1200 820 820 820 820 1200 550 550 550 550 1200 490 490 490 490 1200
Podemos ver cómo el valor más grande del vector desciende a la última componente. Empleamos una variable auxiliar (aux) para el proceso de intercambio:
aux := Sueldos[f]; Sueldos[f] := Sueldos[f+1]; Sueldos[f+1] := aux;
Al salir del for en este ejemplo el contenido del vector es el siguiente:
750 - 820 - 550 - 490 - 1200
Analizando el algoritmo podemos comprobar que el elemento mayor del vector se ubica ahora en el último lugar.
Podemos definir otros vectores con distintos valores y comprobar que siempre el elemento mayor queda al final.
Pero todavía con este algoritmo no se ordena un vector. Solamente está ordenado el último elemento del vector.
Ahora bien, con los 4 elementos que nos quedan podemos hacer el mismo proceso visto anteriormente, con lo cual quedará ordenado otro elemento del vector. Este proceso lo repetiremos hasta que quede ordenado por completo el vector.
Como debemos repetir el mismo algoritmo podemos englobar todo el bloque en otra estructura repetitiva.
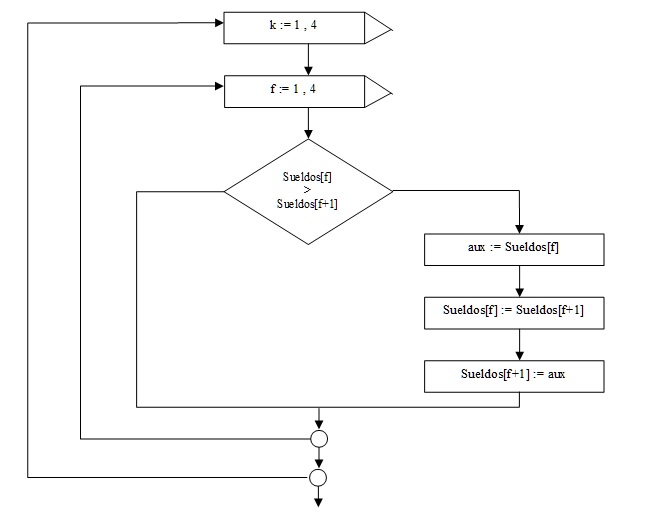
Realicemos una prueba del siguiente algoritmo:
Cuando k = 1
f = 1 f = 2 f = 3 f = 4
750 750 750 750
1200 820 820 820
820 1200 550 550
550 550 1200 490
490 490 490 1200
Cuando h = 2
f = 1 f = 2 f = 3 f = 4
750 750 750 750
820 550 550 550
550 820 490 490
490 490 820 820
1200 1200 1200 1200
Cuando k = 3
f = 1 f = 2 f = 3 f = 4
550 550 550 550
750 490 490 490
490 750 750 750
820 820 820 820
1200 1200 1200 1200
Cuando k = 4
f = 1 f = 2 f = 3 f = 4
490 490 490 490
550 550 550 550
750 750 750 750
820 820 820 820
1200 1200 1200 1200
¿Porque repetimos 4 veces el for externo?
Como sabemos cada vez que se repite en forma completa el for interno queda ordenada una componente del vector. A primera vista diríamos que deberíamos repetir el for externo la cantidad de componentes del vector, en este ejemplo el vector Sueldos tiene 5 componentes.
Si observamos, cuando quedan dos elementos por ordenar al ordenar uno de ellos queda el otro automáticamente ordenado (podemos imaginar que si tenemos un vector con 2 elementos no se requiere el for externo, porque este debería repetirse una única vez).
Una última consideración a este ALGORITMO de ordenamiento es que los elementos que se van ordenando continuamos comparándolos.
Ejemplo: En la primera ejecución del for interno el valor 1200 queda ubicado en la posición 5 del vector. En la segunda ejecución comparamos si el 820 es mayor a 1200, lo cual seguramente será falso.
Podemos concluir que la primera vez debemos hacer para este ejemplo 4 comparaciones, en la segunda ejecución del for interno debemos hacer 3 comparaciones y en general debemos ir reduciendo en uno la cantidad de comparaciones.
Si bien el algoritmo planteado funciona, un algoritmo más eficiente, que se deriva del anterior es el siguiente:
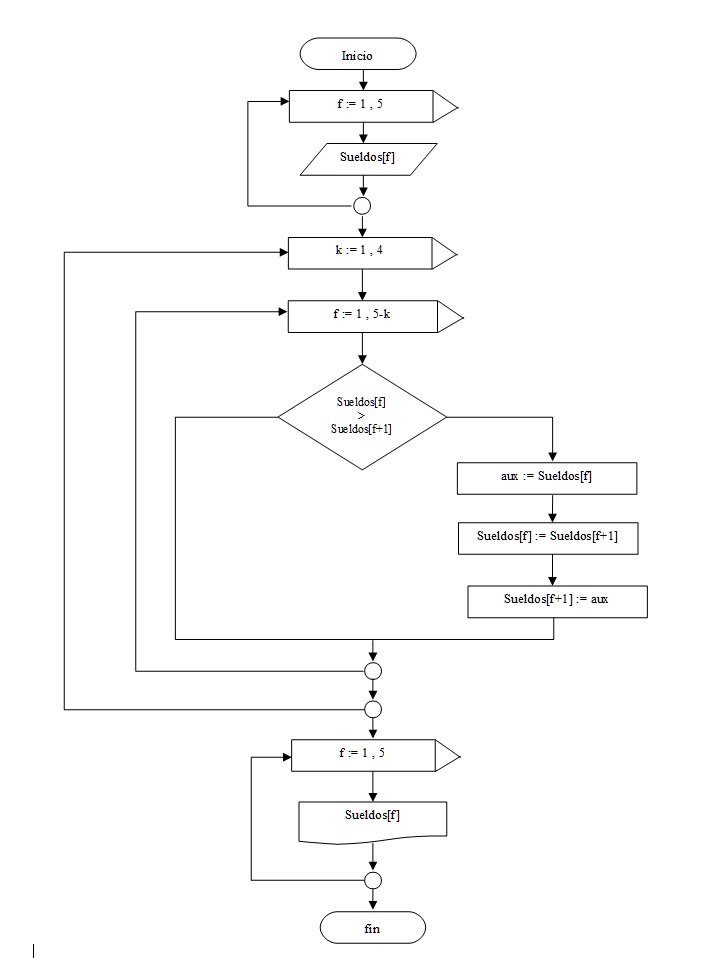
El algoritmo final queda planteado con un for interno que va a ir decreciendo en uno cada vez que el contador del for externo se incremente.
Inicialmente k=1 por lo que el for interno se repite 4 veces (5-k o sea 5-1).
Cuando k=2 el for interno se repite 3 veces, y así sucesivamente.
Proyecto71
program Proyecto71;
{$APPTYPE CONSOLE}
{$R *.res}
type
TSueldos = array[1..5] of Double;
var
sueldos: TSueldos;
f: Integer;
k: Integer;
aux: Double;
Begin
WriteLn('Carga de sueldos');
for f:=1 to 5 do
begin
Write('Ingrese sueldo:');
ReadLn(Sueldos[f]);
end;
for k:=1 to 4 do
begin
for f:=1 to 5-k do
begin
if Sueldos[f] > Sueldos[f+1] then
begin
aux := Sueldos[f];
sueldos[f] := Sueldos[f+1];
Sueldos[f+1] := aux;
end;
end;
end;
WriteLn;
WriteLn('Listado de sueldos ordenados de menor a mayor:');
for f:=1 to 5 do
Begin
Write(Sueldos[f]:0:2,' ');
End;
ReadLn;
end.
La variable aux debe ser del mismo tipo de dato que las componentes del vector (Double), esto es debido a que almacenará temporariamente el contenido de una componente.
La impresión del vector ya ordenado se hace luego de salir de los dos for.
Problema propuesto
- Cargar un vector de 5 elementos Integer. Ordenarlo de mayor a menor y mostrarlo por pantalla, luego ordenar de menor a mayor e imprimir nuevamente
program Proyecto72;
{$APPTYPE CONSOLE}
{$R *.res}
type
TVector = array[1..5] of Integer;
var
Vec: TVector;
f: Integer;
k: Integer;
aux: Integer;
Begin
WriteLn('Carga del vector');
for f:=1 to 5 do
begin
Write('Ingrese componente:');
ReadLn(Vec[f]);
end;
for k:=1 to 4 do
begin
for f:=1 to 5-k do
begin
if Vec[f] < Vec[f+1] then
begin
aux := Vec[f];
Vec[f] := Vec[f+1];
Vec[f+1] := aux;
end;
end;
end;
WriteLn;
WriteLn('Listado del vector ordenados de mayor a menor:');
for f:=1 to 5 do
Begin
Write(Vec[f],' ');
End;
for k:=1 to 4 do
begin
for f:=1 to 5-k do
begin
if Vec[f] > Vec[f+1] then
begin
aux := Vec[f];
Vec[f] := Vec[f+1];
Vec[f+1] := aux;
end;
end;
end;
WriteLn;
WriteLn('Listado del vector ordenados de menor a mayor:');
for f:=1 to 5 do
Begin
Write(Vec[f],' ');
End;
ReadLn;
end.