Árboles en C - Propiedades y medidas

Conocer la altura, la profundidad, la cantidad de hojas y otros indicadores de un árbol binario ayuda a tomar decisiones de balanceo, ajustar heurísticas de búsqueda y validar que la estructura se mantiene saludable. Este tema recopila las propiedades más utilizadas y ofrece fragmentos de código en C para calcularlas.

8.1 Modelo de nodo

Las funciones expuestas trabajan sobre el mismo modelo de nodo usado en los temas anteriores. Si necesitas un campo adicional (por ejemplo, para cachear la altura), puedes adaptarlo siguiendo la misma interfaz.

typedef struct TreeNode {
  int valor;
  struct TreeNode *izquierdo;
  struct TreeNode *derecho;
} TreeNode;

8.2 Altura y profundidad

La altura de un nodo es la cantidad de aristas en el camino más largo hacia una hoja. La profundidad representa la distancia respecto de la raíz. Calcular la altura completa nos permite estimar la complejidad de las operaciones.

int altura(TreeNode *nodo) {
  if (!nodo) return -1;
  int altIzq = altura(nodo->izquierdo);
  int altDer = altura(nodo->derecho);
  return 1 + (altIzq > altDer ? altIzq : altDer);
}

8.3 Conteo de nodos y hojas

El tamaño del árbol se obtiene sumando la cantidad de nodos en cada subárbol. Para contar hojas, verificamos que un nodo no tenga hijos.

unsigned int cantidadNodos(TreeNode *nodo) {
  if (!nodo) return 0;
  return 1 + cantidadNodos(nodo->izquierdo) + cantidadNodos(nodo->derecho);
}

unsigned int cantidadHojas(TreeNode *nodo) {
  if (!nodo) return 0;
  if (!nodo->izquierdo && !nodo->derecho) {
    return 1;
  }
  return cantidadHojas(nodo->izquierdo) + cantidadHojas(nodo->derecho);
}

8.4 Nodos internos y grado

Los nodos internos son aquellos que poseen al menos un hijo. Podemos calcular cuántos hay y, si es necesario, clasificar el grado (cantidad de hijos).

unsigned int nodosInternos(TreeNode *nodo) {
  if (!nodo || (!nodo->izquierdo && !nodo->derecho)) {
    return 0;
  }
  return 1 + nodosInternos(nodo->izquierdo) + nodosInternos(nodo->derecho);
}

8.5 Factor de balance

El factor de balance se define como la diferencia entre la altura del subárbol izquierdo y el derecho. Un valor cercano a cero indica un árbol equilibrado.

int factorBalance(TreeNode *nodo) {
  if (!nodo) return 0;
  return altura(nodo->izquierdo) - altura(nodo->derecho);
}

8.6 Ancho por niveles

El ancho máximo indica cuántos nodos se encuentran en el nivel más poblado. Podemos calcularlo con un recorrido por niveles:

unsigned int anchoMaximo(TreeNode *raiz) {
  if (!raiz) return 0;
  TreeNode *cola[128];
  unsigned int frente = 0, fondo = 0;
  unsigned int maxAncho = 0;
  cola[fondo++] = raiz;

  while (frente < fondo) {
    unsigned int nivelActual = fondo - frente;
    if (nivelActual > maxAncho) {
      maxAncho = nivelActual;
    }
    for (unsigned int i = 0; i < nivelActual; i++) {
      TreeNode *nodo = cola[frente++];
      if (nodo->izquierdo) cola[fondo++] = nodo->izquierdo;
      if (nodo->derecho) cola[fondo++] = nodo->derecho;
    }
  }
  return maxAncho;
}

8.7 Profundidad de un valor

Para conocer la profundidad de un determinado valor seguimos el mismo camino que en una búsqueda y contamos el número de aristas recorridas.

int profundidad(TreeNode *nodo, int valor) {
  int nivel = 0;
  while (nodo) {
    if (valor == nodo->valor) {
      return nivel;
    }
    nivel++;
    nodo = (valor < nodo->valor) ? nodo->izquierdo : nodo->derecho;
  }
  return -1; /* no encontrado */
}

8.8 Resumen operativo

Combinar estas funciones permite monitorear el estado del árbol: si el factor de balance se dispara, se planifica un rebalanceo; si la cantidad de hojas disminuye drásticamente, conviene verificar que la inserción no esté sesgando los datos.

8.9 Código completo para CLion

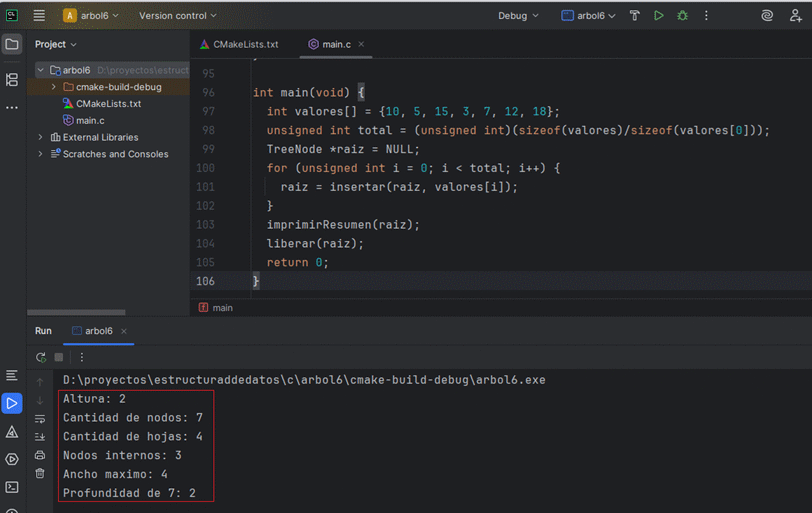
El siguiente programa arma un árbol, calcula todas las medidas y las imprime en consola.

#include <stdio.h>
#include <stdlib.h>

typedef struct TreeNode {
  int valor;
  struct TreeNode *izquierdo;
  struct TreeNode *derecho;
} TreeNode;

TreeNode *crearNodo(int valor) {
  TreeNode *nodo = malloc(sizeof(TreeNode));
  if (!nodo) return NULL;
  nodo->valor = valor;
  nodo->izquierdo = NULL;
  nodo->derecho = NULL;
  return nodo;
}

TreeNode *insertar(TreeNode *raiz, int valor) {
  if (!raiz) return crearNodo(valor);
  if (valor < raiz->valor) {
    raiz->izquierdo = insertar(raiz->izquierdo, valor);
  } else {
    raiz->derecho = insertar(raiz->derecho, valor);
  }
  return raiz;
}

int altura(TreeNode *nodo) {
  if (!nodo) return -1;
  int altIzq = altura(nodo->izquierdo);
  int altDer = altura(nodo->derecho);
  return 1 + (altIzq > altDer ? altIzq : altDer);
}

unsigned int cantidadNodos(TreeNode *nodo) {
  if (!nodo) return 0;
  return 1 + cantidadNodos(nodo->izquierdo) + cantidadNodos(nodo->derecho);
}

unsigned int cantidadHojas(TreeNode *nodo) {
  if (!nodo) return 0;
  if (!nodo->izquierdo && !nodo->derecho) return 1;
  return cantidadHojas(nodo->izquierdo) + cantidadHojas(nodo->derecho);
}

unsigned int nodosInternos(TreeNode *nodo) {
  if (!nodo || (!nodo->izquierdo && !nodo->derecho)) return 0;
  return 1 + nodosInternos(nodo->izquierdo) + nodosInternos(nodo->derecho);
}

unsigned int anchoMaximo(TreeNode *raiz) {
  if (!raiz) return 0;
  TreeNode *cola[128];
  unsigned int frente = 0, fondo = 0;
  unsigned int maxAncho = 0;
  cola[fondo++] = raiz;
  while (frente < fondo) {
    unsigned int nivelActual = fondo - frente;
    if (nivelActual > maxAncho) maxAncho = nivelActual;
    for (unsigned int i = 0; i < nivelActual; i++) {
      TreeNode *nodo = cola[frente++];
      if (nodo->izquierdo) cola[fondo++] = nodo->izquierdo;
      if (nodo->derecho) cola[fondo++] = nodo->derecho;
    }
  }
  return maxAncho;
}

int profundidad(TreeNode *nodo, int valor) {
  int nivel = 0;
  while (nodo) {
    if (valor == nodo->valor) return nivel;
    nivel++;
    nodo = (valor < nodo->valor) ? nodo->izquierdo : nodo->derecho;
  }
  return -1;
}

void imprimirResumen(TreeNode *raiz) {
  printf("Altura: %d\n", altura(raiz));
  printf("Cantidad de nodos: %u\n", cantidadNodos(raiz));
  printf("Cantidad de hojas: %u\n", cantidadHojas(raiz));
  printf("Nodos internos: %u\n", nodosInternos(raiz));
  printf("Ancho maximo: %u\n", anchoMaximo(raiz));
  printf("Profundidad de 7: %d\n", profundidad(raiz, 7));
}

void liberar(TreeNode *nodo) {
  if (!nodo) return;
  liberar(nodo->izquierdo);
  liberar(nodo->derecho);
  free(nodo);
}

int main(void) {
  int valores[] = {10, 5, 15, 3, 7, 12, 18};
  unsigned int total = (unsigned int)(sizeof(valores)/sizeof(valores[0]));
  TreeNode *raiz = NULL;
  for (unsigned int i = 0; i < total; i++) {
    raiz = insertar(raiz, valores[i]);
  }
  imprimirResumen(raiz);
  liberar(raiz);
  return 0;
}

Retornar

8 - Propiedades y medidas del árbol