1 - Introducción a los árboles en estructuras de datos

Iniciamos el tutorial con los conceptos esenciales para comprender cómo se modela un árbol binario y por qué sigue siendo una de las estructuras preferidas al programar en Python. A lo largo de los próximos temas trabajaremos exclusivamente con árboles binarios; los árboles generales quedarán para un curso independiente.

Este capítulo define el vocabulario básico, compara los árboles frente a otras estructuras, explica su utilidad práctica y recopila aplicaciones reales que justifican invertir tiempo en dominarlos.

1.1 ¿Qué es un árbol en estructuras de datos?

Un árbol es un conjunto de nodos conectados mediante aristas direccionales que forman una jerarquía sin ciclos. Existe un único nodo superior llamado raíz y cada nodo puede dar lugar a uno o más descendientes. Si restringimos la cantidad de hijos a lo sumo dos, obtenemos el árbol binario que guia este tutorial.

En Python, cada nodo se implementa con una clase que almacena el dato y referencias hacia los hijos. El siguiente ejemplo resume la plantilla que utilizaremos repetidamente:

class Nodo:
    def __init__(self, valor):
        self.valor = valor
        self.izquierdo = None
        self.derecho = None


def crear_nodo(valor):
    return Nodo(valor)

La función crear_nodo encapsula la creación de la instancia y deja las referencias a hijos en None para evitar estados indeterminados. Esta práctica simplifica la construcción de árboles binarios, su posterior modificación y la liberación ordenada cuando el recolector de basura detecte que no quedan referencias.

1.2 Diferencias entre árboles, listas y grafos

Contrastar los árboles con otras estructuras de datos aclara sus ventajas:

• Listas: estructuras lineales sin bifurcaciones; cada nodo tiene un antecesor y un sucesor como máximo. Ofrecen simplicidad pero un costo de búsqueda lineal obligado.
• Grafos: permiten ciclos, enlaces arbitrarios y distintas ponderaciones. Son versátiles, pero la ausencia de jerarquía fija complejiza los algoritmos.
• Árboles binarios: combinan jerarquía con restricciones claras (a lo sumo dos hijos). Esto aporta caminos deterministas, recorridos bien definidos y varias optimizaciones para operaciones de búsqueda.

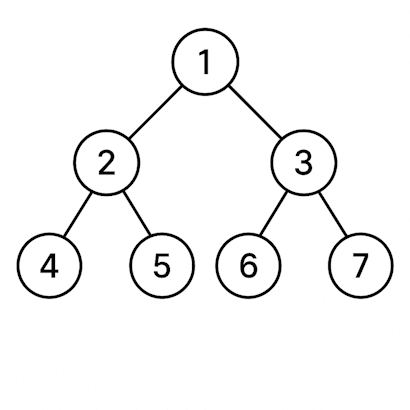
1.3 Terminología esencial

Utilizaremos los siguientes términos de manera consistente:

Raíz

Nodo inicial de la estructura. Desde aquí parten todos los recorridos y no tiene padre.

Nodo

Unidad mínima que contiene el dato y las referencias hacia sus hijos.

Hijos

Nodos directamente conectados y situados un nivel por debajo de su padre. En un árbol binario existen, como máximo, hijo izquierdo e hijo derecho.

Padre

Nodo inmediatamente superior a un conjunto de hijos. Define el orden y las decisiones del subárbol.

Hoja

Nodo sin hijos. Representa un estado final o un dato indivisible dentro del árbol.

1.4 Por qué se usan árboles en informática

Los árboles binarios permiten resolver varios problemas cotidianos:

• Modelar jerarquías: carpetas, permisos y representaciones gráficas siguen una estructura natural de raíz y ramas.
• Acelerar búsquedas: los árboles de búsqueda binarios equilibrados ofrecen desempeño logarítmico.
• Descomponer decisiones: cada bifurcación codifica una pregunta o condición, lo que aporta claridad en reglas de negocio.
• Controlar memoria: en Python las referencias solo se crean cuando es necesario, adaptando el tamaño de la estructura al problema y delegando la liberación al recolector de basura.

1.5 Aplicaciones reales

Algunos casos en los que los árboles binarios se utilizan de forma habitual son:

• Compiladores: construyen árboles de sintaxis abstracta para analizar y optimizar el código fuente.
• Sistemas de archivos: la organización jerárquica de carpetas se representa como un árbol binario o general, según la implementación del sistema operativo.
• Inteligencia artificial: árboles de decisión, minimax y podas alfa-beta exploran movimientos posibles en juegos o clasifican datos.
• Bases de datos: las variaciones de B-Trees y árboles AVL mantienen índices balanceados con excelente desempeño al leer desde disco.

Este recorrido inicial nos deja listos para, en los temas siguientes, diseñar las operaciones fundamentales de inserción, recorrido y búsqueda exclusivamente sobre árboles binarios.