3 - Modelado de nodos en Python
Para programar un árbol binario necesitamos una representación de los nodos que sea consistente, fácil de inicializar y sencilla de limpiar. En este tema diseñamos la clase base y construimos utilidades que conectan hijos, actualizan niveles y mantienen el estado del árbol sin referencias colgantes.
3.1 Estructura del nodo
El nodo almacena el dato y las referencias a cada hijo junto con el nivel actual. Con esa información podemos reconstruir la jerarquía sin depender de referencias adicionales y mantener la estructura ligera.
class Nodo:
def __init__(self, valor, nivel=0):
self.valor = valor
self.izquierdo = None
self.derecho = None
self.nivel = nivel
Mantener la estructura compacta y sin referencia explícita al padre simplifica el modelo y reduce el tamaño total del árbol.
3.2 Contenedor del árbol e inicialización
Centralizamos la raíz y la cantidad de nodos en una clase contenedora. Esta práctica simplifica la detección de árboles vacíos y el seguimiento del tamaño.
class ArbolBinarioOrdenado:
def __init__(self):
self.raiz = None
self.cantidad = 0
Siempre que la referencia a la raíz valga None consideramos al árbol vacío; cualquier inserción crea la nueva raíz.
3.3 Funciones de creación
Las funciones de creación ahora viven dentro de la clase ArbolBinarioOrdenado. Devuelven instancias listas para usar, con referencias a hijos inicializadas en None. Las siguientes utilidades cubren tanto la creación genérica como la inserción de la raíz.
class ArbolBinarioOrdenado:
def __init__(self):
self.raiz = None
self.cantidad = 0
def crear_nodo(self, valor, nivel=0):
return Nodo(valor, nivel=nivel)
def crear_raiz(self, valor):
if self.raiz:
return self.raiz
self.raiz = self.crear_nodo(valor)
self.cantidad = 1
return self.raiz
Separar la creación de la raíz evita errores cuando el árbol ya posee nodos.
3.4 Inserción genérica no recursiva
La inserción sin recursión se apoya en comparaciones: avanzamos por la rama izquierda si el valor es menor al nodo actual, o por la derecha en caso contrario. Una vez que encontramos una referencia nula, enlazamos el nuevo nodo y actualizamos su nivel.
class ArbolBinarioOrdenado:
# ...
def insertar(self, valor):
if self.raiz is None:
return self.crear_raiz(valor)
actual = self.raiz
while True:
if valor < actual.valor:
if actual.izquierdo is None:
actual.izquierdo = self.crear_nodo(valor, nivel=actual.nivel + 1)
self.cantidad += 1
return actual.izquierdo
actual = actual.izquierdo
else:
if actual.derecho is None:
actual.derecho = self.crear_nodo(valor, nivel=actual.nivel + 1)
self.cantidad += 1
return actual.derecho
actual = actual.derecho
Asignar duplicados a la rama derecha mantiene la rutina simple y evita reacomodar nodos; más adelante podremos ajustar esta regla según las necesidades del algoritmo.
3.5 Ejemplo de inserción manual
Para validar el modelado conviene crear un pequeño escenario donde agregamos valores y verificamos el resultado con un recorrido en preorden. Observa cómo los nodos se distribuyen hacia la izquierda cuando el valor insertado es menor.
class ArbolBinarioOrdenado:
# ...
def imprimir_preorden(self, nodo):
if nodo is None:
return
print(f"{nodo.valor} (nivel {nodo.nivel})")
self.imprimir_preorden(nodo.izquierdo)
self.imprimir_preorden(nodo.derecho)
def poblar_arbol(arbol):
for valor in (10, 5, 20, 3, 7):
arbol.insertar(valor)
El recorrido confirma que los niveles y referencias quedaron correctamente sincronizados.
3.6 Liberación segura de memoria
Una vez que terminamos de utilizar el árbol conviene limpiar las referencias para que el recolector de basura pueda liberar la memoria sin ciclos innecesarios. El siguiente helper recorre en postorden y elimina los enlaces desde la propia clase.
class ArbolBinarioOrdenado:
# ...
def liberar_subarbol(self, nodo):
if nodo is None:
return
self.liberar_subarbol(nodo.izquierdo)
self.liberar_subarbol(nodo.derecho)
nodo.izquierdo = None
nodo.derecho = None
def limpiar_arbol(self):
self.liberar_subarbol(self.raiz)
self.raiz = None
self.cantidad = 0
Antes de salir del programa o al reconstruir la estructura, llamamos a limpiar_arbol para evitar referencias residuales.
Contar con estas piezas nos permite abordar el siguiente tema: construir árboles binarios completos a partir de entradas reales sin perder consistencia en los nodos.
3.7 Código completo listo para Python 3
El siguiente archivo corre directamente con Python 3. Reúne las funciones vistas en el tema, crea un árbol de ejemplo y muestra su recorrido en preorden.
class Nodo:
def __init__(self, valor, nivel=0):
self.valor = valor
self.izquierdo = None
self.derecho = None
self.nivel = nivel
class ArbolBinarioOrdenado:
def __init__(self):
self.raiz = None
self.cantidad = 0
def crear_nodo(self, valor, nivel=0):
return Nodo(valor, nivel=nivel)
def crear_raiz(self, valor):
if self.raiz:
return self.raiz
self.raiz = self.crear_nodo(valor)
self.cantidad = 1
return self.raiz
def insertar(self, valor):
if self.raiz is None:
return self.crear_raiz(valor)
actual = self.raiz
while True:
if valor < actual.valor:
if actual.izquierdo is None:
actual.izquierdo = self.crear_nodo(valor, nivel=actual.nivel + 1)
self.cantidad += 1
return actual.izquierdo
actual = actual.izquierdo
else:
if actual.derecho is None:
actual.derecho = self.crear_nodo(valor, nivel=actual.nivel + 1)
self.cantidad += 1
return actual.derecho
actual = actual.derecho
def imprimir_preorden(self, nodo):
if nodo is None:
return
print(f"{nodo.valor} (nivel {nodo.nivel})")
self.imprimir_preorden(nodo.izquierdo)
self.imprimir_preorden(nodo.derecho)
def liberar_subarbol(self, nodo):
if nodo is None:
return
self.liberar_subarbol(nodo.izquierdo)
self.liberar_subarbol(nodo.derecho)
nodo.izquierdo = None
nodo.derecho = None
def limpiar_arbol(self):
self.liberar_subarbol(self.raiz)
self.raiz = None
self.cantidad = 0
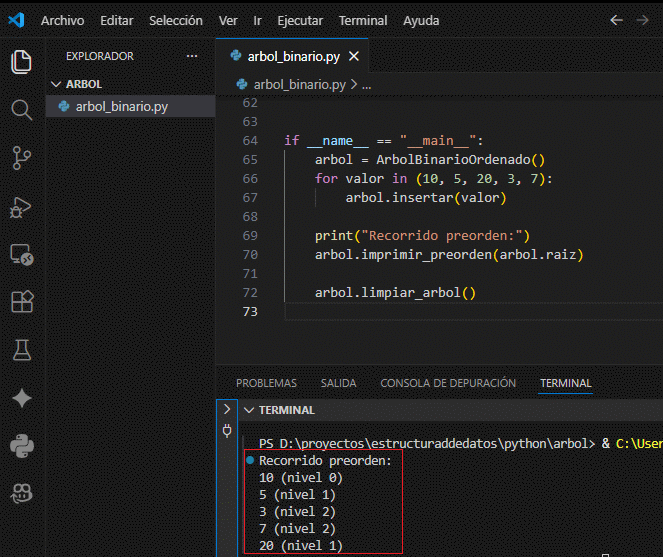
if __name__ == "__main__":
arbol = ArbolBinarioOrdenado()
for valor in (10, 5, 20, 3, 7):
arbol.insertar(valor)
print("Recorrido preorden:")
arbol.imprimir_preorden(arbol.raiz)
arbol.limpiar_arbol()