Arboles B y B+ en C - Inserción

Insertar en un B-Tree exige mantener los límites de claves por nodo. El patrón general es descender solo por nodos que no estén llenos; si un nodo está completo se divide antes de seguir. Esto evita llegar a una hoja saturada.

Visualizador interactivo de Árbol B

5.1 Inserción en nodo hoja no lleno

Si la hoja donde debe ir la clave tiene menos de 2t - 1 claves:

Se desplazan a la derecha las claves mayores para abrir espacio.
Se inserta la nueva clave manteniendo el orden.
No se realizan operaciones sobre el resto del árbol.

5.2 Inserción recursiva en nodo interno

Si el nodo actual es interno:

Se localiza el hijo que contiene el rango de la clave.
Antes de descender, si ese hijo está lleno se hace split para liberar espacio.
Luego se desciende al hijo adecuado (izquierdo o derecho según la clave promovida).

Dividir antes de descender garantiza que siempre lleguemos a una hoja con espacio.

5.3 Operación de split en nodo lleno

Al dividir un nodo con 2t - 1 claves:

Se crea un nuevo nodo hermano con las últimas t - 1 claves.
La clave central (posición t - 1) se promueve al padre.
Si el nodo era interno, se reparten también sus punteros a hijos (t y t).

5.4 Promoción de la clave al nodo padre

La clave media sube al padre y separa a los dos nodos resultantes. En el padre se inserta como cualquier clave, moviendo punteros para colocar los nuevos hijos izquierdo y derecho.

Esta promoción puede encadenarse si el padre estaba lleno, provocando splits hacia arriba hasta, eventualmente, la raíz.

5.5 Casos especiales con la raíz

La raíz tiene dos consideraciones:

Si está llena y se va a insertar, se crea una nueva raíz vacía y se divide la raíz antigua en dos hijos.
Si el árbol está vacío, la raíz es una hoja que recibe la primera clave sin dividir.

Gracias a esto la altura solo crece hacia arriba en splits de la raíz, manteniendo todas las hojas al mismo nivel.

/* Insercion top-down: divide antes de descender */
void btree_insertar(BTreeNode **raiz, int clave) {
  if (*raiz == NULL) return;
  if ((*raiz)->cuenta == 2 * (*raiz)->orden - 1) {
    BTreeNode *nueva = btree_crear((*raiz)->orden);
    nueva->esHoja = 0;
    nueva->hijos[0] = *raiz;
    dividir_hijo(nueva, 0, *raiz);
    *raiz = nueva;
  }
  insertar_no_lleno(*raiz, clave);
}

La función insertar_no_lleno toma decisiones locales (descender o insertar en hoja) asumiendo que el nodo recibido tiene espacio. Esta estrategia top-down evita retroceder después de detectar un nodo lleno.

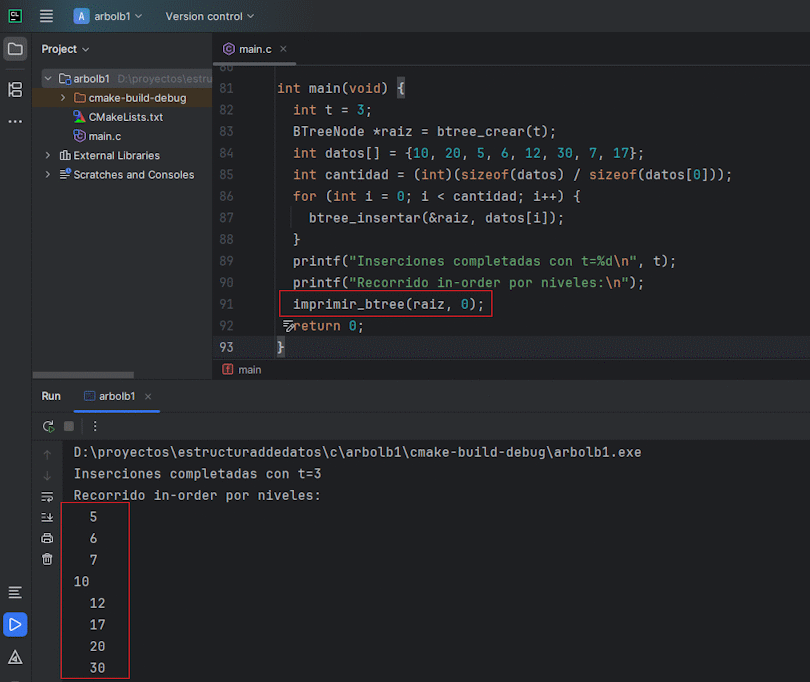
5.6 Código completo para CLion

Ejemplo autocontenido en un solo archivo main.c listo para compilar en CLion o con gcc main.c:

#include <stdio.h>
#include <stdlib.h>

typedef struct BTreeNode {
  int *claves;
  struct BTreeNode **hijos;
  int cuenta;
  int esHoja;
  int orden;
} BTreeNode;

static BTreeNode *btree_crear(int t) {
  BTreeNode *n = malloc(sizeof(BTreeNode));
  n->orden = t;
  n->esHoja = 1;
  n->cuenta = 0;
  n->claves = malloc(sizeof(int) * (2 * t - 1));
  n->hijos = malloc(sizeof(BTreeNode *) * (2 * t));
  return n;
}

static void dividir_hijo(BTreeNode *padre, int idx, BTreeNode *hijo) {
  int t = hijo->orden;
  BTreeNode *nuevo = btree_crear(t);
  nuevo->esHoja = hijo->esHoja;
  nuevo->cuenta = t - 1;
  for (int j = 0; j < t - 1; j++) nuevo->claves[j] = hijo->claves[j + t];
  if (!hijo->esHoja) {
    for (int j = 0; j < t; j++) nuevo->hijos[j] = hijo->hijos[j + t];
  }
  hijo->cuenta = t - 1;
  for (int j = padre->cuenta; j >= idx + 1; j--) padre->hijos[j + 1] = padre->hijos[j];
  padre->hijos[idx + 1] = nuevo;
  for (int j = padre->cuenta - 1; j >= idx; j--) padre->claves[j + 1] = padre->claves[j];
  padre->claves[idx] = hijo->claves[t - 1];
  padre->cuenta++;
}

static void insertar_no_lleno(BTreeNode *nodo, int clave) {
  int i = nodo->cuenta - 1;
  if (nodo->esHoja) {
    while (i >= 0 && clave < nodo->claves[i]) {
      nodo->claves[i + 1] = nodo->claves[i];
      i--;
    }
    nodo->claves[i + 1] = clave;
    nodo->cuenta++;
  } else {
    while (i >= 0 && clave < nodo->claves[i]) i--;
    i++;
    if (nodo->hijos[i]->cuenta == 2 * nodo->orden - 1) {
      dividir_hijo(nodo, i, nodo->hijos[i]);
      if (clave > nodo->claves[i]) i++;
    }
    insertar_no_lleno(nodo->hijos[i], clave);
  }
}

void btree_insertar(BTreeNode **raiz, int clave) {
  if (*raiz == NULL) return;
  if ((*raiz)->cuenta == 2 * (*raiz)->orden - 1) {
    BTreeNode *nueva = btree_crear((*raiz)->orden);
    nueva->esHoja = 0;
    nueva->hijos[0] = *raiz;
    dividir_hijo(nueva, 0, *raiz);
    *raiz = nueva;
  }
  insertar_no_lleno(*raiz, clave);
}

static void imprimir_btree(BTreeNode *nodo, int nivel) {
  if (!nodo) return;
  for (int i = 0; i < nodo->cuenta; i++) {
    if (!nodo->esHoja) imprimir_btree(nodo->hijos[i], nivel + 1);
    for (int j = 0; j < nivel; j++) printf("  ");
    printf("%d\n", nodo->claves[i]);
  }
  if (!nodo->esHoja) imprimir_btree(nodo->hijos[nodo->cuenta], nivel + 1);
}

int main(void) {
  int t = 3;
  BTreeNode *raiz = btree_crear(t);
  int datos[] = {10, 20, 5, 6, 12, 30, 7, 17};
  int cantidad = (int)(sizeof(datos) / sizeof(datos[0]));
  for (int i = 0; i < cantidad; i++) {
    btree_insertar(&raiz, datos[i]);
  }
  printf("Inserciones completadas con t=%d\n", t);
  printf("Recorrido in-order por niveles:\n");
  imprimir_btree(raiz, 0);
  return 0;
}