Arboles B y B+ en C - Operaciones en árboles B+

Las operaciones en un árbol B+ conservan la altura baja y explotan las hojas enlazadas para recorridos secuenciales rápidos. Las reglas de llenado y división son similares al B-Tree, pero la diferencia clave es que las claves se almacenan solo en hojas.

Visualizador interactivo de Árbol B+

8.1 Búsqueda

Se recorre desde la raíz comparando con las claves internas hasta llegar a una hoja.
La coincidencia se verifica solo en la hoja; los internos sirven como límites superiores.
Complejidad O(h) con altura típicamente 2 o 3 en índices reales.

8.2 Inserción

Se desciende hasta la hoja adecuada; si está llena, se divide antes de insertar.
La clave promovida al padre es la primera clave del nuevo nodo hoja derecho.
Se mantienen los enlaces entre hojas actualizando punteros de vecino al dividir.

8.3 Split en nodos hoja

Dividir una hoja llena (2t claves) crea dos hojas con t claves cada una:

La clave de promoción al interno padre es la menor clave del nuevo nodo derecho.
Los punteros de siguiente/anterior se ajustan para mantener la lista enlazada.
Los datos permanecen en hojas; los internos no almacenan registros.

8.4 Redistribución

Si un nodo hoja tiene déficit, puede tomar claves de un hermano con espacio (≥ t).
La clave separadora en el padre se actualiza para reflejar la nueva mínima del hijo derecho.
Redistribuir evita fusionar y mantiene la ocupación sin aumentar la altura.

8.5 Eliminación

Se borra en la hoja; si queda con menos de t - 1 claves, se redistribuye o fusiona con un hermano.
Si se fusiona, se elimina la clave separadora en el padre y se encadena la lista de hojas.
Si la raíz queda sin claves y tiene un solo hijo, ese hijo se convierte en la nueva raíz.

8.6 Recorrido eficiente por hojas enlazadas

Para un range scan se baja una vez por el árbol hasta la primera hoja en el rango.
Luego se itera hoja a hoja usando los punteros de enlace, sin volver a los nodos internos.
Esto ofrece complejidad O(h + k) para devolver k resultados consecutivos.

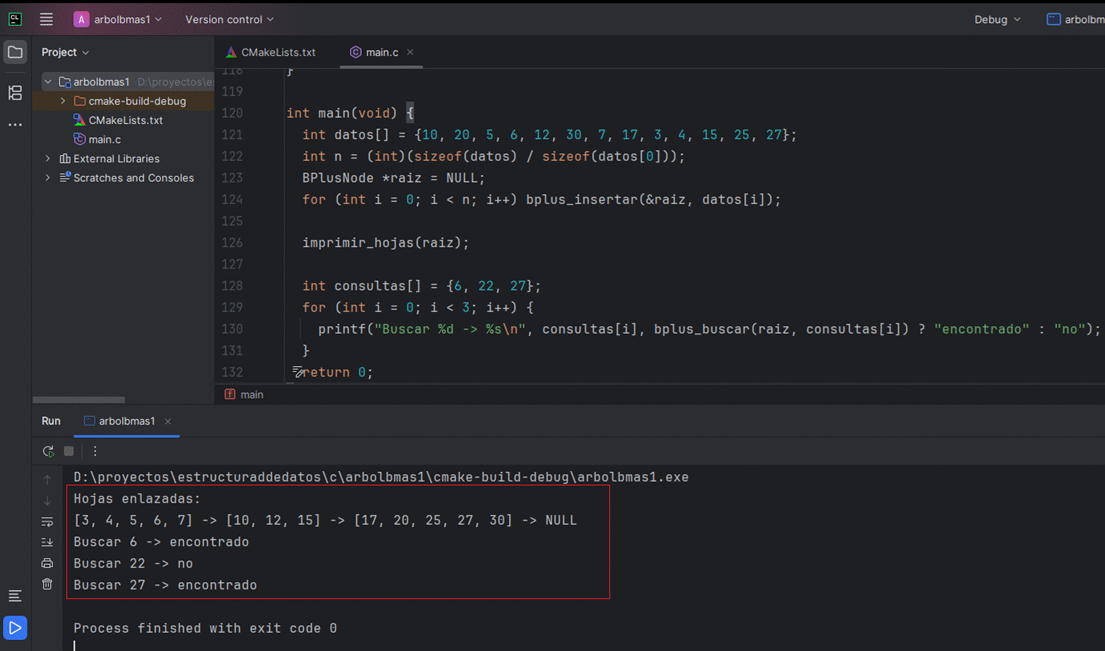
8.7 Código completo para probar en CLion

Ejemplo autocontenido en main.c con inserción, búsqueda y recorrido por hojas enlazadas en un árbol B+:

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define ORDEN 3
#define MAX_CLAVES (2 * ORDEN - 1)
#define MAX_HIJOS (2 * ORDEN)

typedef struct BPlusNode {
  int claves[MAX_CLAVES];
  struct BPlusNode *hijos[MAX_HIJOS];
  struct BPlusNode *siguiente; /* solo para hojas */
  int cuenta;
  int esHoja;
} BPlusNode;

static BPlusNode *crear_nodo(int esHoja) {
  BPlusNode *n = calloc(1, sizeof(BPlusNode));
  n->esHoja = esHoja;
  return n;
}

static int buscar_posicion(BPlusNode *n, int clave) {
  int i = 0;
  while (i < n->cuenta && clave > n->claves[i]) i++;
  return i;
}

static void split_hoja(BPlusNode *padre, int idx, BPlusNode *hijo) {
  BPlusNode *nuevo = crear_nodo(1);
  int mid = hijo->cuenta / 2;
  int mover = hijo->cuenta - mid;
  memcpy(nuevo->claves, hijo->claves + mid, mover * sizeof(int));
  nuevo->cuenta = mover;
  hijo->cuenta = mid;

  nuevo->siguiente = hijo->siguiente;
  hijo->siguiente = nuevo;

  for (int j = padre->cuenta; j >= idx + 1; j--) padre->hijos[j + 1] = padre->hijos[j];
  padre->hijos[idx + 1] = nuevo;
  for (int j = padre->cuenta - 1; j >= idx; j--) padre->claves[j + 1] = padre->claves[j];
  padre->claves[idx] = nuevo->claves[0]; /* clave de promoción en B+ */
  padre->cuenta++;
}

static void split_interno(BPlusNode *padre, int idx, BPlusNode *hijo) {
  BPlusNode *nuevo = crear_nodo(0);
  int mid = hijo->cuenta / 2;
  int promover = hijo->claves[mid];

  nuevo->cuenta = hijo->cuenta - mid - 1;
  for (int j = 0; j < nuevo->cuenta; j++) nuevo->claves[j] = hijo->claves[mid + 1 + j];
  for (int j = 0; j <= nuevo->cuenta; j++) nuevo->hijos[j] = hijo->hijos[mid + 1 + j];

  hijo->cuenta = mid;

  for (int j = padre->cuenta; j >= idx + 1; j--) padre->hijos[j + 1] = padre->hijos[j];
  padre->hijos[idx + 1] = nuevo;
  for (int j = padre->cuenta - 1; j >= idx; j--) padre->claves[j + 1] = padre->claves[j];
  padre->claves[idx] = promover;
  padre->cuenta++;
}

static void insertar_no_lleno(BPlusNode *nodo, int clave) {
  int pos = buscar_posicion(nodo, clave);
  if (nodo->esHoja) {
    for (int j = nodo->cuenta; j > pos; j--) nodo->claves[j] = nodo->claves[j - 1];
    nodo->claves[pos] = clave;
    nodo->cuenta++;
  } else {
    BPlusNode *hijo = nodo->hijos[pos];
    if (hijo->cuenta == MAX_CLAVES) {
      if (hijo->esHoja) split_hoja(nodo, pos, hijo);
      else split_interno(nodo, pos, hijo);
      if (clave >= nodo->claves[pos]) hijo = nodo->hijos[pos + 1];
    }
    insertar_no_lleno(hijo, clave);
  }
}

void bplus_insertar(BPlusNode **raiz, int clave) {
  if (*raiz == NULL) {
    *raiz = crear_nodo(1);
    (*raiz)->claves[0] = clave;
    (*raiz)->cuenta = 1;
    return;
  }
  if ((*raiz)->cuenta == MAX_CLAVES) {
    BPlusNode *nueva = crear_nodo(0);
    nueva->hijos[0] = *raiz;
    if ((*raiz)->esHoja) split_hoja(nueva, 0, *raiz);
    else split_interno(nueva, 0, *raiz);
    *raiz = nueva;
  }
  insertar_no_lleno(*raiz, clave);
}

int bplus_buscar(BPlusNode *nodo, int clave) {
  if (!nodo) return 0;
  int pos = buscar_posicion(nodo, clave);
  if (nodo->esHoja) return pos < nodo->cuenta && nodo->claves[pos] == clave;
  return bplus_buscar(nodo->hijos[pos], clave);
}

void imprimir_hojas(BPlusNode *raiz) {
  if (!raiz) return;
  while (!raiz->esHoja) raiz = raiz->hijos[0];
  printf("Hojas enlazadas:\n");
  for (BPlusNode *n = raiz; n; n = n->siguiente) {
    printf("[");
    for (int i = 0; i < n->cuenta; i++) {
      printf("%d%s", n->claves[i], i + 1 == n->cuenta ? "" : ", ");
    }
    printf("] -> ");
  }
  printf("NULL\n");
}

int main(void) {
  int datos[] = {10, 20, 5, 6, 12, 30, 7, 17, 3, 4, 15, 25, 27};
  int n = (int)(sizeof(datos) / sizeof(datos[0]));
  BPlusNode *raiz = NULL;
  for (int i = 0; i < n; i++) bplus_insertar(&raiz, datos[i]);

  imprimir_hojas(raiz);

  int consultas[] = {6, 22, 27};
  for (int i = 0; i < 3; i++) {
    printf("Buscar %d -> %s\n", consultas[i], bplus_buscar(raiz, consultas[i]) ? "encontrado" : "no");
  }
  return 0;
}

Retornar