3 - Representaciones de árboles generales en C
Tras definir los componentes de un árbol n-ario, necesitamos elegir la estructura de datos que represente los hijos de cada nodo dentro de C. En este tema contrastamos las alternativas más utilizadas, estudiando sus costos de memoria, facilidad de inserción y compatibilidad con los algoritmos que desarrollaremos en los próximos temas.
3.1 Problemas de la representación clásica
Si reutilizamos el struct de un árbol binario y simplemente agregamos más punteros (hijo1, hijo2, hijo3, ...), obtenemos una estructura estática que no escala. Aparecen los siguientes inconvenientes:
- Memoria desperdiciada: cada nodo reserva espacio para todos los punteros aunque no tenga tantos hijos.
- Inserción costosa: hay que encontrar un campo libre entre los punteros predefinidos o rediseñar la estructura si un nodo supera el límite.
- Dificultad para recorridos: los algoritmos deben conocer la cantidad exacta de punteros declarados para iterar sobre ellos, lo que vuelve difícil reutilizar funciones genéricas.
Por eso reemplazaremos esta representación fija por estructuras flexibles que adapten el número de enlaces a las necesidades del árbol.
3.2 Representación con lista dinámica de hijos
Una solución simple consiste en mantener una lista enlazada de hijos por nodo. Cada elemento de la lista referencia al nodo hijo real, y la cabecera reside dentro del nodo padre. Esta opción es clara y mantiene separados los datos del nodo y los del contenedor de hijos.
#include <stdlib.h>
typedef struct GeneralNode GeneralNode;
typedef struct ChildNode {
GeneralNode *nodo;
struct ChildNode *siguiente;
} ChildNode;
struct GeneralNode {
int valor;
ChildNode *hijos;
};
ChildNode *crearChildNode(GeneralNode *nodo) {
ChildNode *child = malloc(sizeof(ChildNode));
if (!child) {
return NULL;
}
child->nodo = nodo;
child->siguiente = NULL;
return child;
}
void agregarHijoLista(GeneralNode *padre, GeneralNode *nuevoHijo) {
if (!padre || !nuevoHijo) {
return;
}
ChildNode *child = crearChildNode(nuevoHijo);
if (!child) {
return;
}
child->siguiente = padre->hijos;
padre->hijos = child;
}Con esta representación, insertar es tan fácil como enlazar un nuevo elemento al inicio de la lista. El costo principal es recorrer la lista para obtener el n-ésimo hijo o liberar los nodos auxiliares.
3.3 Representación con arrays de hijos (grado fijo)
Cuando el grado máximo es conocido y pequeño, un array de punteros simplifica el acceso directo a cualquier hijo. Declaramos una constante con el grado y mantenemos un contador del número de posiciones ocupadas. Esta estrategia es eficiente en elementos compactos como nodos de un arreglo dinámico especializado.
#include <stdlib.h>
#define MAX_HIJOS 4
typedef struct GeneralNode {
int valor;
unsigned int cantidadHijos;
struct GeneralNode *hijos[MAX_HIJOS];
} GeneralNode;
GeneralNode *crearNodoArray(int valor) {
GeneralNode *nodo = malloc(sizeof(GeneralNode));
if (!nodo) {
return NULL;
}
nodo->valor = valor;
nodo->cantidadHijos = 0;
for (unsigned int i = 0; i < MAX_HIJOS; ++i) {
nodo->hijos[i] = NULL;
}
return nodo;
}
int agregarHijoArray(GeneralNode *padre, GeneralNode *nuevoHijo) {
if (!padre || !nuevoHijo || padre->cantidadHijos >= MAX_HIJOS) {
return 0;
}
padre->hijos[padre->cantidadHijos++] = nuevoHijo;
return 1;
}Utilizar arreglos permite indexar hijos inmediatamente, pero limita la cantidad de descendientes y obliga a copiar o mover punteros si queremos insertar en posiciones intermedias.
3.4 Representación eficiente: Left-Child Right-Sibling
El patrón hijo-izquierdo/hermano-derecho (LCRS) convierte cualquier árbol n-ario en un árbol binario donde el puntero primerHijo actúa como enlace hacia el subárbol más profundo y siguienteHermano enlaza los nodos laterales. Esta representación se integra perfectamente con los recorridos recursivos y requiere solo dos punteros por nodo. Vimos en el concepto anterior su implementación.
#include <stdlib.h>
typedef struct GeneralNode {
int valor;
struct GeneralNode *primerHijo;
struct GeneralNode *siguienteHermano;
struct GeneralNode *padre;
} GeneralNode;
GeneralNode *crearNodoLCRS(int valor) {
GeneralNode *nodo = malloc(sizeof(GeneralNode));
if (!nodo) {
return NULL;
}
nodo->valor = valor;
nodo->primerHijo = NULL;
nodo->siguienteHermano = NULL;
nodo->padre = NULL;
return nodo;
}
void insertarHijoLCRS(GeneralNode *padre, GeneralNode *nuevoHijo) {
if (!padre || !nuevoHijo) {
return;
}
nuevoHijo->padre = padre;
nuevoHijo->siguienteHermano = padre->primerHijo;
padre->primerHijo = nuevoHijo;
}Para recorrer a todos los hijos de un nodo basta con iterar sobre la cadena de hermanos. Los algoritmos de borrado o copia se implementan como operaciones binarias, lo que simplifica enormemente la recursión.
3.5 Ventajas de cada representación
- Lista dinámica: no impone un límite de hijos, permite inserciones y borrados en O(1) al inicio de la lista y separa claramente el nodo de la administración de hijos.
- Array fijo: ofrece acceso directo por índice, un layout compacto en memoria y cache-friendly cuando el grado es pequeño y estable.
- LCRS: utiliza solo dos punteros por nodo, reusa funciones pensadas para árboles binarios y facilita la conversión a representaciones secuenciales.
La elección depende del escenario: si esperamos nodos con cientos de hijos, la lista o LCRS son superiores; si solo existen hasta 3 o 4 hijos y necesitamos accederlos por posición, el array fijo es práctico.
3.6 Cuándo elegir cada representación
- Escenarios exploratorios: durante la construcción inicial del árbol conviene LCRS, porque permite reutilizar herramientas del tutorial de árboles binarios y facilita depurar punteros.
- Modelos de configuración: si un nodo debe enumerar opciones en orden y el grado está acotado, el array fijo mantiene la lógica simple y evita nodos auxiliares.
- Estructuras editables: para editores de escenas, árboles DOM o directorios, la lista de hijos delega en una estructura separada la inserción, borrado y ordenamiento, ofreciendo la mayor flexibilidad.
- Conversiones o exportaciones: cuando sea necesario serializar el árbol, LCRS produce una forma compacta que se guarda con dos punteros por nodo y se transforma fácilmente en representaciones binarias.
En la práctica veremos que no existe una opción universal; lo importante es documentar la elección y encapsular las operaciones para poder migrar entre representaciones sin reescribir todo el código.
3.7 Aplicación completa con lista dinámica de hijos
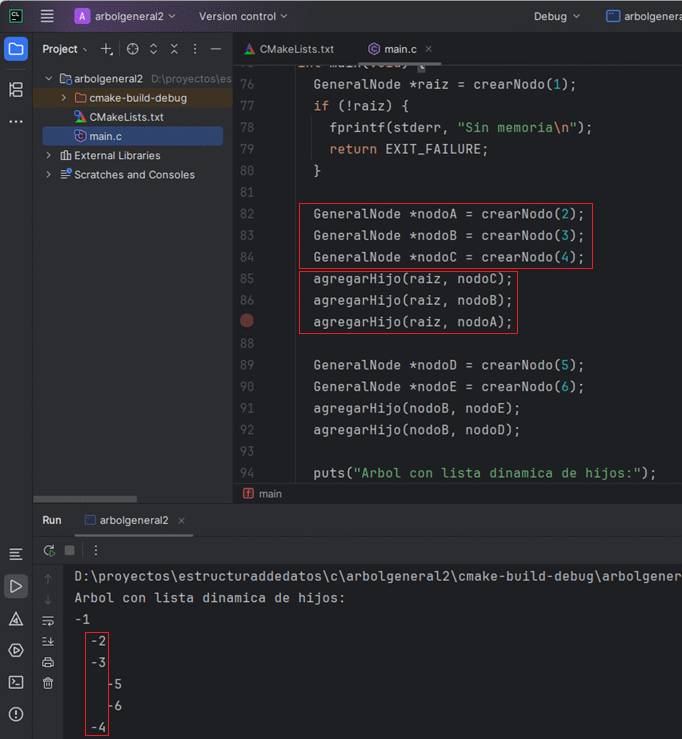
Para poner en práctica la representación con listas de hijos, a continuación presentamos un programa listo para ejecutar en CLion. El ejemplo crea un árbol general, imprime su contenido y libera toda la memoria reservada.
#include <stdio.h>
#include <stdlib.h>
typedef struct GeneralNode GeneralNode;
typedef struct ChildNode {
GeneralNode *nodo;
struct ChildNode *siguiente;
} ChildNode;
struct GeneralNode {
int valor;
ChildNode *hijos;
};
GeneralNode *crearNodo(int valor) {
GeneralNode *nodo = malloc(sizeof(GeneralNode));
if (!nodo) {
return NULL;
}
nodo->valor = valor;
nodo->hijos = NULL;
return nodo;
}
ChildNode *crearChildNode(GeneralNode *nodo) {
ChildNode *child = malloc(sizeof(ChildNode));
if (!child) {
return NULL;
}
child->nodo = nodo;
child->siguiente = NULL;
return child;
}
void agregarHijo(GeneralNode *padre, GeneralNode *nuevoHijo) {
if (!padre || !nuevoHijo) {
return;
}
ChildNode *child = crearChildNode(nuevoHijo);
if (!child) {
return;
}
child->siguiente = padre->hijos;
padre->hijos = child;
}
void imprimirArbol(const GeneralNode *nodo, unsigned int sangria) {
if (!nodo) {
return;
}
for (unsigned int i = 0; i < sangria; ++i) {
printf(" ");
}
printf("-%d\n", nodo->valor);
for (ChildNode *child = nodo->hijos; child; child = child->siguiente) {
imprimirArbol(child->nodo, sangria + 1);
}
}
void destruirArbol(GeneralNode *nodo) {
if (!nodo) {
return;
}
ChildNode *child = nodo->hijos;
while (child) {
ChildNode *siguiente = child->siguiente;
destruirArbol(child->nodo);
free(child);
child = siguiente;
}
free(nodo);
}
int main(void) {
GeneralNode *raiz = crearNodo(1);
if (!raiz) {
fprintf(stderr, "Sin memoria\n");
return EXIT_FAILURE;
}
GeneralNode *nodoA = crearNodo(2);
GeneralNode *nodoB = crearNodo(3);
GeneralNode *nodoC = crearNodo(4);
agregarHijo(raiz, nodoC);
agregarHijo(raiz, nodoB);
agregarHijo(raiz, nodoA);
GeneralNode *nodoD = crearNodo(5);
GeneralNode *nodoE = crearNodo(6);
agregarHijo(nodoB, nodoE);
agregarHijo(nodoB, nodoD);
puts("Arbol con lista dinamica de hijos:");
imprimirArbol(raiz, 0);
destruirArbol(raiz);
return EXIT_SUCCESS;
}El programa demuestra cómo insertar hijos en cualquier orden, recorrerlos con recursión y liberar los nodos auxiliares de la lista sin fugas de memoria.