1 - Introducción a los árboles generales en estructuras de datos

Extendemos la base del curso previo de árboles binarios y nos enfocamos ahora en los árboles generales o n-arios, estructuras donde cada nodo puede contar con un número arbitrario de hijos. Todo el análisis se implementa en Python, aprovechando referencias, recolección de basura y las mismas convenciones de tutoriales anteriores.

Este primer tema respalda el vocabulario elemental, contrasta las diferencias con los árboles de dos hijos, expone la terminología que reutilizaremos y ejemplifica las ventajas de trabajar con ramas ilimitadas. También revisamos casos reales donde un árbol general es la elección natural.

1.1 ¿Qué es un árbol general o n-ario?

Un árbol general es una colección jerárquica de nodos unida por aristas dirigidas sin ciclos, donde cada nodo puede tener cero, uno o muchos hijos. Al igual que en los árboles binarios, existe un nodo raíz único y el resto de los nodos se distribuye en niveles según su distancia a la raíz. La diferencia clave radica en que no imponemos límites a la cantidad de descendientes por nodo.

Para reutilizar lo aprendido, mantenemos el mismo Nodo del curso previo y lo adaptamos a una lista de hijos. En Python trabajaremos con listas (o diccionarios si necesitamos claves), lo que elimina la complejidad de reservar arreglos fijos. También veremos una variante con el patrón left-child right-sibling cuando necesitemos compatibilidad con estructuras heredadas.

class Nodo:
  def __init__(self, valor):
    self.valor = valor
    self.hijos = []  # lista de referencias a nodos hijos

  def agregar_hijo(self, nodo_hijo):
    if nodo_hijo is None:
      return
    self.hijos.append(nodo_hijo)


# ejemplo de uso
if __name__ == "__main__":
  raiz = Nodo("raiz")
  raiz.agregar_hijo(Nodo("A"))
  raiz.agregar_hijo(Nodo("B"))
  raiz.hijos[0].agregar_hijo(Nodo("A1"))
  raiz.hijos[0].agregar_hijo(Nodo("A2"))

El método agregar_hijo apoya la extensión natural de la estructura sin preocuparnos por la liberación manual de memoria; el recolector de basura retirará los nodos no referenciados. Para recorridos recursivos, bastará con iterar sobre hijos.

1.2 Diferencias con árboles binarios

Aunque ambos comparten la idea de una jerarquía sin ciclos, existen diferencias prácticas que debemos tener presentes desde el diseño:

• Número de enlaces: los nodos binarios fijan dos referencias (izquierdo y derecho), mientras que un nodo general usa listas o el esquema hijo-izquierdo/hermano-derecho para sostener cualquier cantidad de hijos.
• Recorridos: los recorridos clásicos (preorden, postorden) requieren ajustes porque el orden de hijos ya no está atado a izquierda y derecha sino a la secuencia de la lista.
• Operaciones de inserción: agregar un hijo nuevo en un árbol general implica decidir su posición relativa respecto a los demás hermanos; en Python basta con insertar en la lista en el índice deseado.
• Aplicaciones: un árbol binario suele ser ideal para búsqueda y ordenamiento; uno general representa mejor estructuras cuyo número de ramas varía: taxonomías, escenas, directorios, modelos de decisiones complejos y más.

1.3 Terminología esencial

Para evitar ambigüedades, estas son las definiciones que utilizaremos durante todo el tutorial:

Raíz general

Nodo superior de la estructura, almacenado en la variable raiz como hicimos con los árboles binarios.

Padre e hijos

Un nodo es padre de todos los que dependen de su lista hijos; cada hijo puede tener a su vez sus propios descendientes.

Hermanos

Nodos que comparten el mismo padre. El orden en la lista de hijos define el orden de recorrido.

Subárbol

Estructura formada por un nodo y todos los descendientes alcanzables desde él. Eliminarlos implica liberar un conjunto completo de nodos.

Grado

Número de hijos de un nodo. El grado máximo del árbol describe cuántas ramas puede albergar cualquier nivel.

Nivel y altura

El nivel de un nodo corresponde a su distancia desde la raíz; la altura es el nivel máximo alcanzado. Nos sirve para estimar el costo de los recorridos.

Bosque

Conjunto de árboles generales independientes. Convertiremos un bosque en un único árbol al crear una raíz ficticia.

1.4 Ventajas en estructuras flexibles

Adoptar árboles generales trae beneficios concretos cuando la cantidad de hijos es variable:

• Escalabilidad natural: no es necesario reservar filas completas de referencias como en los arreglos estáticos; se agregan nodos solo cuando hace falta.
• Reutilización de utilidades: el patrón hijo-izquierdo/hermano-derecho mantiene nombres familiares (raiz, izquierdo, derecho) y permite adaptar funciones del tutorial de binarios.
• Modelado fidedigno: jerarquías complejas, como configuraciones o escenas de videojuegos, pueden conservar todos los niveles reales sin forzar duplicados vacíos.
• Interoperabilidad: exportar la estructura a formatos como JSON o XML resulta directo porque cada nodo almacena colecciones de hijos.

1.5 Aplicaciones reales: directorios, DOM, JSON, IA, juegos

Los árboles generales son esenciales en varios dominios:

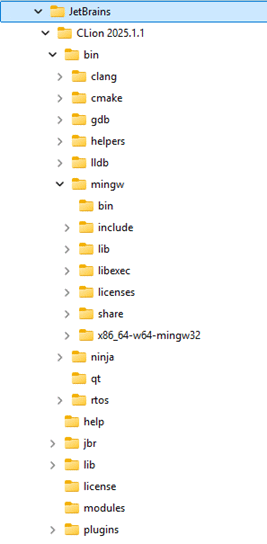
• Sistemas de archivos: los directorios anidados se representan como un árbol en los sistemas de archivos, donde cada carpeta puede contener innumerables elementos.
  
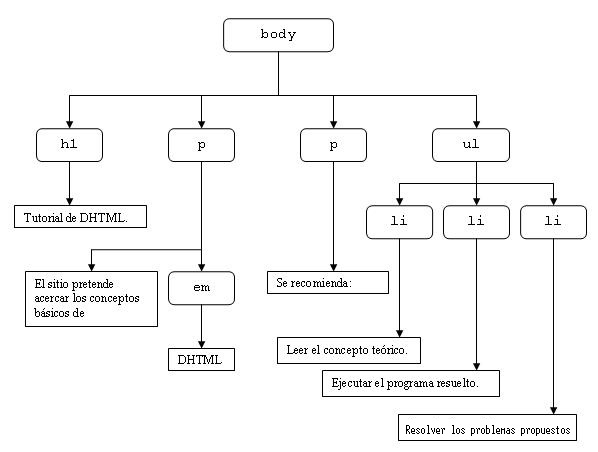
• DOM: el Document Object Model describe la estructura jerárquica de una página HTML con nodos que tienen cualquier cantidad de hijos.
  
• JSON: los documentos definidos por JSON se interpretan como árboles generales donde cada objeto y arreglo agrega ramas arbitrarias.
• Inteligencia artificial: modelos como los árboles de decisión o los árboles de juego de IA requieren nodos con fan-out variable para representar alternativas.
• Videojuegos: diálogos ramificados, misiones secundarias y árboles de habilidades almacenan cada opción como un hijo nuevo sin limitarse a dos caminos.

Con estas definiciones y motivaciones sentadas podremos profundizar en las representaciones y algoritmos específicos en los próximos temas.