2 - Componentes y propiedades de un árbol general
Profundizamos en cada elemento que describe a un árbol general: cómo se define el nodo, de qué manera se enlazan las aristas, cuál es el impacto de los subárboles y cómo medir propiedades como grado, altura y estado vacío. Mantendremos la convención de nombres introducida en el primer tema para que cualquier fragmento sea fácil de reusar en Python.
2.1 Nodos
El nodo general debe tolerar cualquier cantidad de hijos. Una estrategia habitual consiste en almacenar referencias al primer hijo y al siguiente hermano, además de un enlace opcional al padre para simplificar recorridos ascendentes. Conservamos el campo valor y dejamos las referencias en None al crear la estructura.
class Nodo:
def __init__(self, valor):
self.valor = valor
self.primer_hijo = None
self.siguiente_hermano = None
self.padre = NoneEste diseño replica la semántica de izquierdo y derecho del tutorial de árboles binarios, lo que facilita adaptar código existente y convertir entre representaciones.
2.2 Aristas
Las aristas definen las conexiones entre padres e hijos. En un árbol general, cada nueva arista se agrega enlazando el hijo dentro de la cadena de descendientes y ajustando la referencia al padre.
class ArbolGeneral:
def __init__(self):
self.raiz = None
self.cantidad = 0
def enlazar_como_primer_hijo(self, padre, nuevo_hijo):
if padre is None or nuevo_hijo is None:
return
nuevo_hijo.padre = padre
nuevo_hijo.siguiente_hermano = padre.primer_hijo
padre.primer_hijo = nuevo_hijo
def enlazar_como_hermano(self, referencia, nuevo_hermano):
if referencia is None or nuevo_hermano is None:
return
nuevo_hermano.padre = referencia.padre
nuevo_hermano.siguiente_hermano = referencia.siguiente_hermano
referencia.siguiente_hermano = nuevo_hermanoLlevar el control de estas aristas nos permite recorrer hijos linealmente, reordenar ramas y detectar inconsistencias antes de ejecutar algoritmos más costosos.
2.3 Raíz, hijos y hermanos
La raíz es el nodo superior y punto de entrada del árbol. Desde ella obtenemos cualquier hijo siguiendo la referencia primer_hijo. Cada hijo a su vez posee un enlace a su hermano inmediato mediante siguiente_hermano. Estas tres piezas bastan para reconstruir todo el arbolado y permiten operar tanto vertical como horizontalmente.
En los recorridos es común alternar una iteración mientras existan hermanos y, dentro de cada hermano, entrar de forma recursiva a sus respectivos hijos. Este patrón asegura que no dejamos ramas aisladas.
2.4 Subárboles
Un subárbol está formado por un nodo y todos sus descendientes. Trabajar con subárboles facilita tareas como clonar secciones, mover ramas completas o limpiar referencias de forma localizada. La función siguiente recorre un subárbol y acumula sus nodos.
class ArbolGeneral:
...
def contar_subarbol(self, nodo):
if nodo is None:
return 0
total = 1
hijo = nodo.primer_hijo
while hijo:
total += self.contar_subarbol(hijo)
hijo = hijo.siguiente_hermano
return totalEste recorrido sirve de base para borrar subárboles, serializarlos o calcular alturas locales.
2.5 Número de hijos (grado del nodo)
El grado describe cuántos hijos directos posee un nodo. En árboles generales un grado alto indica fan-out elevado y, por ende, mayor costo de memoria para esa rama. Se obtiene contando los nodos en la lista de hijos.
class ArbolGeneral:
...
def grado_nodo(self, nodo):
grado = 0
hijo = nodo.primer_hijo if nodo else None
while hijo:
grado += 1
hijo = hijo.siguiente_hermano
return gradoGuardar el grado nos ayuda a dimensionar estructuras auxiliares, validar que un nodo respete un límite de hijos o ajustar heurísticas de balance.
2.6 Altura y profundidad
La profundidad de un nodo es la cantidad de aristas que lo separan de la raíz; la altura del árbol es la profundidad máxima encontrada. Estos valores influyen en la complejidad de las operaciones, especialmente cuando se recorre todo el árbol.
class ArbolGeneral:
...
def profundidad(self, nodo):
nivel = 0
while nodo and nodo.padre:
nodo = nodo.padre
nivel += 1
return nivel
def altura(self, nodo):
if nodo is None:
return 0
max_hijos = 0
hijo = nodo.primer_hijo
while hijo:
altura_hijo = self.altura(hijo)
max_hijos = max(max_hijos, altura_hijo)
hijo = hijo.siguiente_hermano
return 1 + max_hijosCalcular estas medidas periódicamente permite detectar ramas que crecen sin control y decidir si conviene normalizarlas.
2.7 Árbol vacío y árbol no vacío
Diferenciar entre un árbol vacío y uno con nodos activos evita accesos indebidos. Centralizamos esta información en un contenedor que registra la raíz y el total de nodos administrados.
class ArbolGeneral:
def __init__(self):
self.raiz = None
self.cantidad = 0
def esta_vacio(arbol):
return arbol is None or arbol.raiz is NoneAl encapsular la raíz podemos crear funciones de inserción que incrementen cantidad y detectar si las operaciones dejan el árbol en estado inconsistente.
2.8 Representación gráfica
Visualizar el árbol ayuda a depurar y documentar. Sin depender de librerías externas podemos imprimir una representación textual con indentaciones, simulando un diagrama jerárquico. Cada nivel se desplaza algunos espacios para reflejar la profundidad.
class ArbolGeneral:
...
def imprimir_arbol(self, nodo=None, sangria=0):
nodo = nodo or self.raiz
if nodo is None:
return
print(" " * sangria + f"-{nodo.valor}")
hijo = nodo.primer_hijo
while hijo:
self.imprimir_arbol(hijo, sangria + 1)
hijo = hijo.siguiente_hermanoEste mismo patrón puede adaptarse para generar diagramas ASCII o exportar datos en formatos aptos para herramientas de visualización. En Python no necesitamos liberar memoria manualmente; basta con eliminar referencias a las raíces de los subárboles para que el recolector actúe.
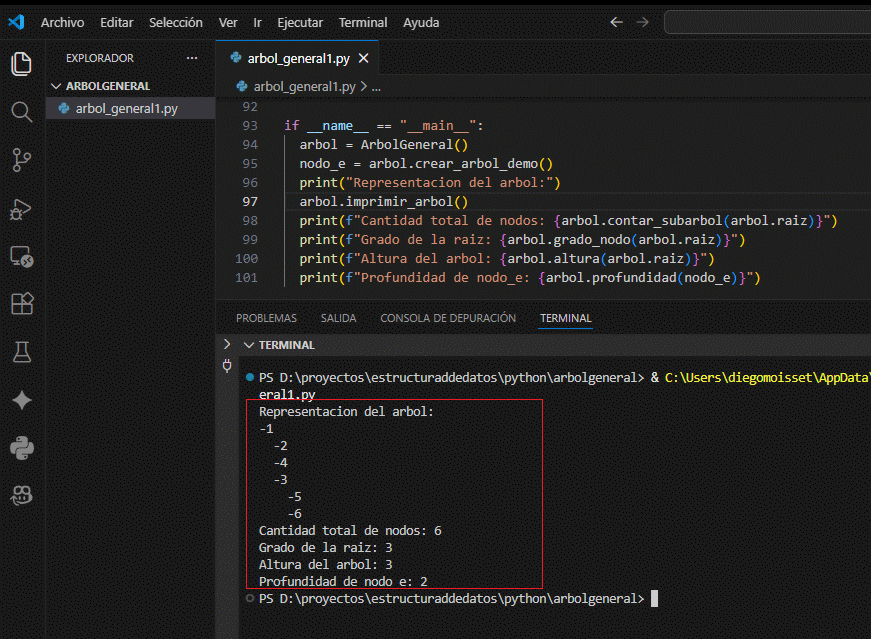
Para cerrar este tema incluimos un archivo completo listo para ejecutar en VS Code o PyCharm, con la mayoría de los métodos anteriores dentro de la clase ArbolGeneral y un ejemplo de uso:
class Nodo:
def __init__(self, valor):
self.valor = valor
self.primer_hijo = None
self.siguiente_hermano = None
self.padre = None
class ArbolGeneral:
def __init__(self):
self.raiz = None
self.cantidad = 0
def enlazar_como_primer_hijo(self, padre, nuevo_hijo):
if padre is None or nuevo_hijo is None:
return
nuevo_hijo.padre = padre
nuevo_hijo.siguiente_hermano = padre.primer_hijo
padre.primer_hijo = nuevo_hijo
def enlazar_como_hermano(self, referencia, nuevo_hermano):
if referencia is None or nuevo_hermano is None:
return
nuevo_hermano.padre = referencia.padre
nuevo_hermano.siguiente_hermano = referencia.siguiente_hermano
referencia.siguiente_hermano = nuevo_hermano
def contar_subarbol(self, nodo):
if nodo is None:
return 0
total = 1
hijo = nodo.primer_hijo
while hijo:
total += self.contar_subarbol(hijo)
hijo = hijo.siguiente_hermano
return total
def grado_nodo(self, nodo):
grado = 0
hijo = nodo.primer_hijo if nodo else None
while hijo:
grado += 1
hijo = hijo.siguiente_hermano
return grado
def profundidad(self, nodo):
nivel = 0
while nodo and nodo.padre:
nodo = nodo.padre
nivel += 1
return nivel
def altura(self, nodo):
if nodo is None:
return 0
max_hijos = 0
hijo = nodo.primer_hijo
while hijo:
max_hijos = max(max_hijos, self.altura(hijo))
hijo = hijo.siguiente_hermano
return 1 + max_hijos
def imprimir_arbol(self, nodo=None, sangria=0):
nodo = nodo or self.raiz
if nodo is None:
return
print(" " * sangria + f"-{nodo.valor}")
hijo = nodo.primer_hijo
while hijo:
self.imprimir_arbol(hijo, sangria + 1)
hijo = hijo.siguiente_hermano
def crear_arbol_demo(self):
self.raiz = Nodo(1)
self.cantidad = 1
nodo_a = Nodo(2)
nodo_b = Nodo(3)
nodo_c = Nodo(4)
self.enlazar_como_primer_hijo(self.raiz, nodo_b)
self.enlazar_como_primer_hijo(self.raiz, nodo_a)
self.enlazar_como_hermano(nodo_a, nodo_c)
self.cantidad += 3
nodo_d = Nodo(5)
nodo_e = Nodo(6)
self.enlazar_como_primer_hijo(nodo_b, nodo_d)
self.enlazar_como_hermano(nodo_d, nodo_e)
self.cantidad += 2
return nodo_e
if __name__ == "__main__":
arbol = ArbolGeneral()
nodo_e = arbol.crear_arbol_demo()
print("Representacion del arbol:")
arbol.imprimir_arbol()
print(f"Cantidad total de nodos: {arbol.contar_subarbol(arbol.raiz)}")
print(f"Grado de la raiz: {arbol.grado_nodo(arbol.raiz)}")
print(f"Altura del arbol: {arbol.altura(arbol.raiz)}")
print(f"Profundidad de nodo_e: {arbol.profundidad(nodo_e)}")