Colas en C - Colas de prioridad

8.1 Concepto general

Una cola de prioridad atiende primero al elemento con mayor prioridad (o menor coste, según la convención elegida) sin importar el orden de llegada. Mantiene la eficiencia del modelo FIFO en la interfaz pero introduce una relación de orden parcial que requiere estructuras internas específicas.

Se usa en planificadores, routers, simuladores de eventos discretos y algoritmos de grafos como Dijkstra o Prim, donde es vital extraer constantemente el próximo elemento más relevante.

8.2 Interfaz y operaciones

insert o push: incorpora un elemento con su prioridad asociada.
extract o pop: remueve el elemento con mejor prioridad, devolviendo el par valor-prioridad.
peek: consulta el elemento ganador sin extraerlo.
update: opcional; ajusta la prioridad de un elemento existente (decrease-key/increase-key).

Para mantener complejidad logarítmica, la estructura interna suele ser un heap binario almacenado en arreglo continuo.

8.3 Alternativas de implementación

Array desordenado: inserción O(1) y extracción O(n). Útil cuando hay pocas operaciones pop.
Lista ordenada: inserción O(n), extracción O(1). Adecuado para colas muy pequeñas.
Heap binario: insert/extract en O(log n) y peek en O(1). Este es el balance más habitual.
Montículos especializados: binomial, Fibonacci o pairing heap se emplean cuando hay muchas operaciones decrease-key.

En C, el heap binario resulta sencillo de mantener usando índices y operaciones de intercambio.

8.4 Heap binario en arreglo

En un heap almacenado en un array, el padre de un nodo en la posición i se encuentra en (i - 1) / 2 y los hijos en 2 * i + 1 y 2 * i + 2. El siguiente esqueleto funciona como max-heap (mayor prioridad implica mayor valor numérico):

#define CAP_HEAP 256

typedef struct {
  int valor;
  int prioridad;
} NodoPQ;

typedef struct {
  NodoPQ datos[CAP_HEAP];
  int cantidad;
} PriorityQueue;

void pq_init(PriorityQueue *pq) {
  pq->cantidad = 0;
}

static void intercambiar(NodoPQ *a, NodoPQ *b) {
  NodoPQ tmp = *a;
  *a = *b;
  *b = tmp;
}

static void sift_up(PriorityQueue *pq, int idx) {
  while (idx > 0) {
    int padre = (idx - 1) / 2;
    if (pq->datos[idx].prioridad <= pq->datos[padre].prioridad) {
      break;
    }
    intercambiar(&pq->datos[idx], &pq->datos[padre]);
    idx = padre;
  }
}

static void sift_down(PriorityQueue *pq, int idx) {
  while (1) {
    int hijoIzq = 2 * idx + 1;
    int hijoDer = hijoIzq + 1;
    int mayor = idx;
    if (hijoIzq < pq->cantidad && pq->datos[hijoIzq].prioridad > pq->datos[mayor].prioridad) {
      mayor = hijoIzq;
    }
    if (hijoDer < pq->cantidad && pq->datos[hijoDer].prioridad > pq->datos[mayor].prioridad) {
      mayor = hijoDer;
    }
    if (mayor == idx) {
      break;
    }
    intercambiar(&pq->datos[idx], &pq->datos[mayor]);
    idx = mayor;
  }
}

Los helpers sift_up y sift_down mantienen el invariante del heap tras cada inserción o extracción.

8.5 Insertar y extraer

Insertar y extraer requieren validar la capacidad y reubicar nodos para preservar el orden de prioridad:

int pq_push(PriorityQueue *pq, int valor, int prioridad) {
  if (pq->cantidad == CAP_HEAP) {
    return 0;
  }
  int idx = pq->cantidad++;
  pq->datos[idx].valor = valor;
  pq->datos[idx].prioridad = prioridad;
  sift_up(pq, idx);
  return 1;
}

int pq_pop(PriorityQueue *pq, int *valor, int *prioridad) {
  if (pq->cantidad == 0) {
    return 0;
  }
  *valor = pq->datos[0].valor;
  *prioridad = pq->datos[0].prioridad;
  pq->datos[0] = pq->datos[pq->cantidad - 1];
  pq->cantidad--;
  sift_down(pq, 0);
  return 1;
}

int pq_peek(const PriorityQueue *pq, int *valor, int *prioridad) {
  if (pq->cantidad == 0) {
    return 0;
  }
  *valor = pq->datos[0].valor;
  *prioridad = pq->datos[0].prioridad;
  return 1;
}

El costo amortizado se mantiene en O(log n) gracias a las funciones de sift. Si se necesitan prioridades mínimas se intercambia la comparación (> por <).

8.6 Comparadores y estabilidad

Algunos escenarios requieren usar criterios compuestos (por ejemplo, mayor prioridad numérica pero, en caso de empate, menor tiempo de llegada). En esos casos conviene encapsular la comparación en una función:

typedef struct {
  int prioridad;
  unsigned long llegada;
  int valor;
} ElementoPQ;

static int cmp(const ElementoPQ *a, const ElementoPQ *b) {
  if (a->prioridad != b->prioridad) {
    return (a->prioridad > b->prioridad) ? 1 : -1;
  }
  return (a->llegada < b->llegada) ? 1 : -1;
}

El comparador define si la cola es estable. Guardar un contador de llegada facilita romper empates sin perder orden cronológico.

8.7 Casos de uso

Planificación preemptiva: los hilos con mayor prioridad se extraen del heap antes que el resto.
Redes: los paquetes con prioridad QoS alta se envían primero.
Algoritmos de grafos: Dijkstra y A* dependen de una cola de prioridad para seleccionar el próximo nodo con camino parcial más corto.

En todos los casos el diseño define si la prioridad es mutable y cómo se sincroniza el acceso concurrente.

8.8 Ejemplo completo en C

El ejemplo siguiente crea una cola de prioridad de maxima prioridad numérica, inserta varias tareas y luego las procesa en orden:

#include <stdio.h>
#include <stdlib.h>

#define CAP_HEAP 64

typedef struct {
  int valor;
  int prioridad;
} NodoPQ;

typedef struct {
  NodoPQ datos[CAP_HEAP];
  int cantidad;
} PriorityQueue;

void pq_init(PriorityQueue *pq) {
  pq->cantidad = 0;
}

static void swap(NodoPQ *a, NodoPQ *b) {
  NodoPQ tmp = *a;
  *a = *b;
  *b = tmp;
}

static void sift_up(PriorityQueue *pq, int idx) {
  while (idx > 0) {
    int padre = (idx - 1) / 2;
    if (pq->datos[idx].prioridad <= pq->datos[padre].prioridad) {
      break;
    }
    swap(&pq->datos[idx], &pq->datos[padre]);
    idx = padre;
  }
}

static void sift_down(PriorityQueue *pq, int idx) {
  while (1) {
    int mayor = idx;
    int hijoIzq = 2 * idx + 1;
    int hijoDer = hijoIzq + 1;
    if (hijoIzq < pq->cantidad && pq->datos[hijoIzq].prioridad > pq->datos[mayor].prioridad) {
      mayor = hijoIzq;
    }
    if (hijoDer < pq->cantidad && pq->datos[hijoDer].prioridad > pq->datos[mayor].prioridad) {
      mayor = hijoDer;
    }
    if (mayor == idx) {
      break;
    }
    swap(&pq->datos[idx], &pq->datos[mayor]);
    idx = mayor;
  }
}

int pq_push(PriorityQueue *pq, int valor, int prioridad) {
  if (pq->cantidad == CAP_HEAP) {
    return 0;
  }
  int idx = pq->cantidad++;
  pq->datos[idx].valor = valor;
  pq->datos[idx].prioridad = prioridad;
  sift_up(pq, idx);
  return 1;
}

int pq_pop(PriorityQueue *pq, int *valor, int *prioridad) {
  if (pq->cantidad == 0) {
    return 0;
  }
  *valor = pq->datos[0].valor;
  *prioridad = pq->datos[0].prioridad;
  pq->datos[0] = pq->datos[pq->cantidad - 1];
  pq->cantidad--;
  sift_down(pq, 0);
  return 1;
}

void imprimir(const PriorityQueue *pq) {
  printf("[pq] cantidad=%d -> ", pq->cantidad);
  for (int i = 0; i < pq->cantidad; ++i) {
    printf("(%d,%d) ", pq->datos[i].valor, pq->datos[i].prioridad);
  }
  puts("");
}

int main(void) {
  PriorityQueue pq;
  pq_init(&pq);

  pq_push(&pq, 100, 5);
  pq_push(&pq, 20, 1);
  pq_push(&pq, 300, 10);
  pq_push(&pq, 40, 3);
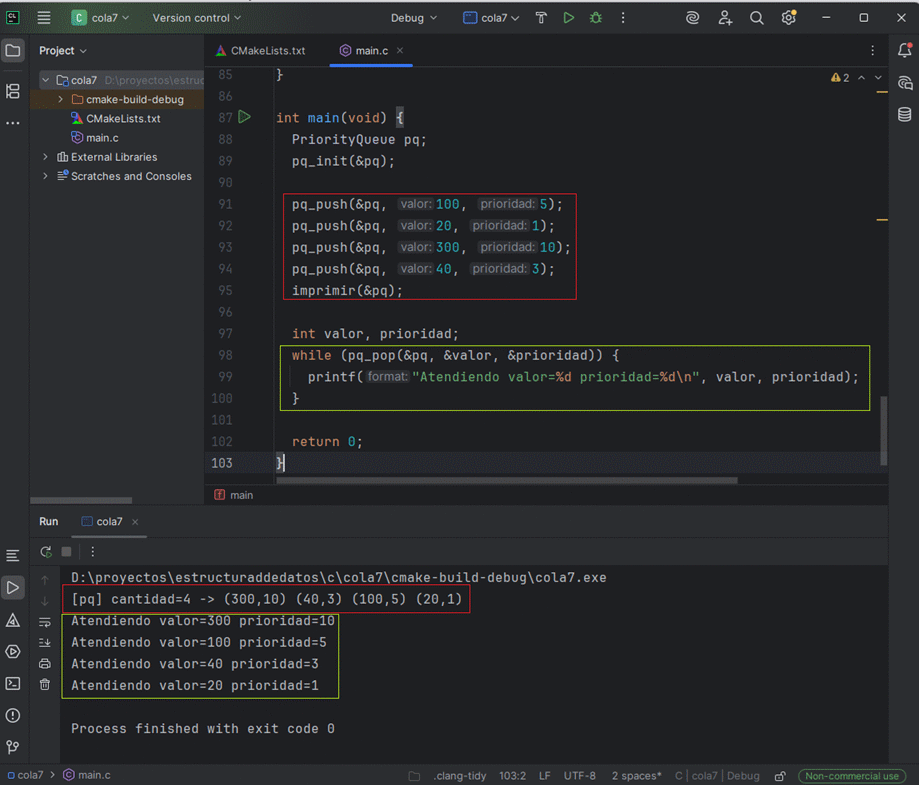
  imprimir(&pq);

  int valor, prioridad;
  while (pq_pop(&pq, &valor, &prioridad)) {
    printf("Atendiendo valor=%d prioridad=%d\n", valor, prioridad);
  }

  return 0;
}

Modifica los valores de prioridad y observa cómo el montículo reorganiza los elementos para mantener siempre el máximo en la raíz.

Diagrama del heap binario mostrando reordenamientos según prioridad

Retornar

8 - Colas de prioridad (Priority Queue)