1 - Introducción a los grafos en estructuras de datos

Iniciamos el tutorial de grafos aclarando el vocabulario y los motivos por los cuales esta estructura es tan flexible en C. A diferencia de las estructuras lineales o jerárquicas, los grafos modelan relaciones arbitrarias y permiten capturar redes, mapas, dependencias y flujos.

Este capítulo define qué es un grafo, la terminología básica, los tipos de problemas que habilita y varias aplicaciones reales que justifican dominarlo.

1.1 ¿Qué es un grafo?

Un grafo es un par G = (V, E) donde V es un conjunto finito de vértices (o nodos) y E es un conjunto de aristas que conectan pares de vértices. Las aristas pueden ser:

• No dirigidas: el enlace no tiene sentido de dirección, la conexión sirve en ambos sentidos.
• Dirigidas: también llamadas arcos, llevan una dirección origen → destino.
• Ponderadas: almacenan un valor numérico (peso o costo) asociado a la conexión.

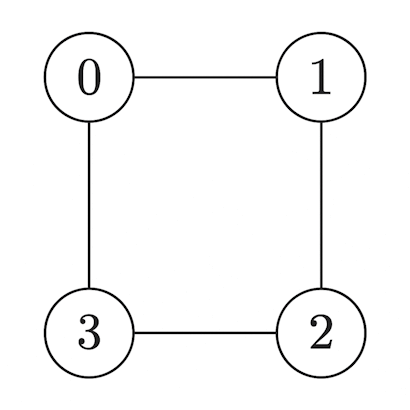
En C es habitual representar un grafo con una matriz de adyacencia o una lista de adyacencia. El siguiente ejemplo muestra una matriz de adyacencia para un grafo no dirigido con 4 vértices:

#include <stdio.h>

int main(void) {
  int n = 4;
  int matriz[4][4] = {
    {0, 1, 0, 1}, /* conexiones del vertice 0 */
    {1, 0, 1, 0},
    {0, 1, 0, 1},
    {1, 0, 1, 0}
  };

  /* Verificamos si 0 y 2 son adyacentes */
  printf("0 y 2 son vecinos? %s\n", matriz[0][2] ? "si" : "no");
  return 0;
}

Una matriz de adyacencia es un arreglo cuadrado de tamaño n x n donde n es la cantidad de vértices. Cada posición [u][v] indica si existe una arista entre los vértices u y v; en grafos no dirigidos la matriz es simétrica y la diagonal suele quedar en 0. Si almacenamos pesos, el valor numérico representa la distancia o costo de la conexión. Su consumo de memoria es O(n²), por lo que resulta práctica en grafos densos (muchas aristas) y menos conveniente en grafos poco poblados.

El valor 1 indica la existencia de una arista entre dos vértices. En la matriz del ejemplo no hay arista directa entre 0 y 2 (el valor es 0), por eso la salida imprime no. Aun así, 0 puede llegar a 2 siguiendo dos saltos: primero hasta 1 y luego hasta 2 (0 → 1 → 2), o primero hasta 3 y luego hasta 2 (0 → 3 → 2). Con pequeñas variaciones este modelo soporta grafos dirigidos (matriz asimétrica) y grafos ponderados (almacenando el peso en lugar de 0/1).

1.2 Terminología básica

Usaremos los siguientes términos de forma consistente a lo largo del tutorial:

Vértices

Elementos o entidades del grafo. Se identifican con índices o etiquetas y guardan el estado que queremos modelar.

Aristas

Conexiones entre vértices. Pueden ser dirigidas o no dirigidas y opcionalmente llevar un peso.

Grado

Número de aristas incidentes a un vértice. En grafos dirigidos se distingue grado de entrada y grado de salida.

Peso

Valor asociado a una arista que representa distancia, costo, capacidad o prioridad.

Adyacencia

Relación que indica si dos vértices están conectados por una arista. En matrices se comprueba con matriz[u][v] != 0.

Camino y ciclo

Un camino es una secuencia de vértices conectados por aristas consecutivas. Un ciclo es un camino que empieza y termina en el mismo vértice sin repetir aristas.

1.3 ¿Qué problemas resuelven los grafos?

Gracias a su flexibilidad, los grafos permiten modelar y resolver problemas variados:

• Rutas y optimización de caminos: búsqueda de rutas más cortas, caminos acotados por capacidad o por restricciones de visita.
• Conectividad y componentes: determinar si un grafo está conectado, contar componentes o detectar puntos de articulación.
• Ordenamiento topológico: programación de tareas con dependencias y detección de ciclos en grafos dirigidos.
• Redes de flujo: maximizar el flujo entre origen y destino cumpliendo capacidades por arista.
• Construcción de árboles generadores: encontrar subconjuntos mínimos de aristas que mantienen conectividad con costo total reducido.

1.4 Aplicaciones reales

Los grafos aparecen en numerosos dominios prácticos:

• Redes de computadoras: routers y switches como vértices, enlaces como aristas ponderadas por ancho de banda o latencia.
• Sistemas de navegación: mapas viales modelados como grafos ponderados para calcular rutas por distancia o tiempo.
• Recomendación y redes sociales: usuarios como nodos y relaciones como aristas; los caminos miden cercanías o influencia.
• Compilación y analizador de dependencias: grafos dirigidos que representan módulos y sus requisitos para ordenar compilaciones.
• Logística y cadenas de suministro: centros de distribución conectados por rutas que se optimizan por costo o capacidad.

Con estos conceptos cubiertos podremos implementar representaciones en C y avanzar hacia algoritmos de recorrido, búsqueda y optimización sobre grafos.