3 - Representaciones de grafos en C

Elegir cómo guardar un grafo en memoria cambia la complejidad de las operaciones. En C predominan dos estructuras: la matriz de adyacencia y la lista de adyacencia. Este tema compara ambas, sus costos y los escenarios donde conviene cada una.

3.1 Matriz de adyacencia

Se usa un arreglo bidimensional n x n donde n es la cantidad de vértices. Cada celda [u][v] indica si existe arista de u a v (o almacena el peso si el grafo es ponderado).

#include <stdio.h>

#define N 4

int main(void) {
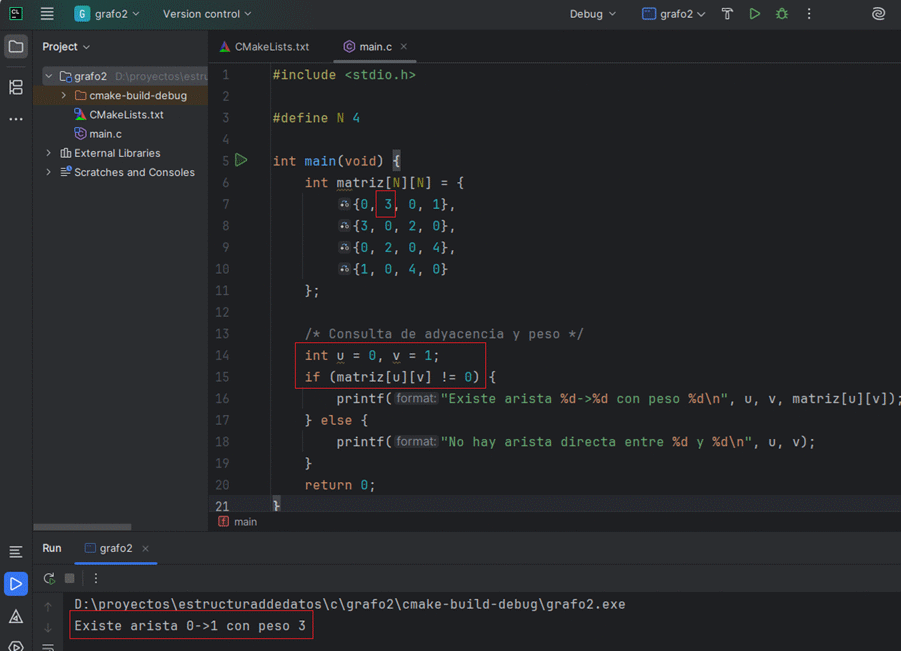
  int matriz[N][N] = {
    {0, 3, 0, 1},
    {3, 0, 2, 0},
    {0, 2, 0, 4},
    {1, 0, 4, 0}
  };

  /* Consulta de adyacencia y peso */
  int u = 0, v = 1;
  if (matriz[u][v] != 0) {
    printf("Existe arista %d->%d con peso %d\n", u, v, matriz[u][v]);
  } else {
    printf("No hay arista directa entre %d y %d\n", u, v);
  }
  return 0;
}

La consulta de adyacencia es O(1) y el código queda compacto. El costo es el consumo de memoria O(n²), incluso si hay pocas aristas.

3.2 Lista de adyacencia

Cada vértice guarda una lista de sus vecinos. Se implementa con arreglos de listas enlazadas o con arreglos de vectores dinámicos.

#include <stdio.h>
#include <stdlib.h>

typedef struct Arista {
  int destino;
  int peso;
  struct Arista *sig;
} Arista;

typedef struct Grafo {
  int n;
  Arista **listas; /* arreglo de punteros a listas */
} Grafo;

Grafo *crearGrafo(int n) {
  Grafo *g = malloc(sizeof(Grafo));
  if (!g) return NULL;
  g->n = n;
  g->listas = calloc(n, sizeof(Arista *));
  return g;
}

void agregarArista(Grafo *g, int u, int v, int peso) {
  Arista *nuevo = malloc(sizeof(Arista));
  if (!nuevo) return;
  nuevo->destino = v;
  nuevo->peso = peso;
  nuevo->sig = g->listas[u];
  g->listas[u] = nuevo;
}

void imprimirVecinos(Grafo *g, int u) {
  printf("Vecinos de %d:", u);
  for (Arista *it = g->listas[u]; it; it = it->sig) {
    printf(" %d(peso=%d)", it->destino, it->peso);
  }
  printf("\n");
}

int main(void) {
  Grafo *g = crearGrafo(4);
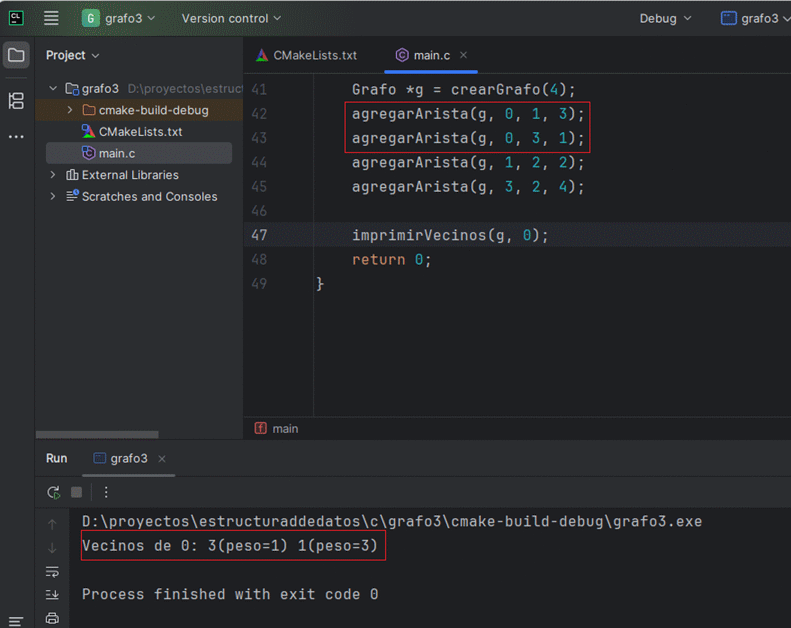
  agregarArista(g, 0, 1, 3);
  agregarArista(g, 0, 3, 1);
  agregarArista(g, 1, 2, 2);
  agregarArista(g, 3, 2, 4);

  imprimirVecinos(g, 0);
  return 0;
}

Con las inserciones anteriores, la lista de vecinos de 0 queda en el orden de inserción inverso (agregamos al frente), por lo que la salida esperada es: Vecinos de 0: 3(peso=1) 1(peso=3).

El uso de memoria es proporcional al número de aristas (O(n + m)). Consultar adyacencia directa requiere recorrer la lista de vecinos de u (O(grado(u))).

3.3 Comparación entre estructuras

• Adyacencia: matriz O(1); lista O(grado(u)).
• Memoria: matriz O(n²); lista O(n + m).
• Iterar vecinos: similar en ambas; la lista ahorra posiciones vacías.
• Mutabilidad: insertar/eliminar aristas es inmediato en lista; en matriz basta asignar pero se paga el costo fijo de n² celdas.

3.4 Costos de memoria en cada representación

En una matriz de enteros de 4 bytes, un grafo con 5.000 vértices ocupa alrededor de 95 MB aunque tenga pocas aristas. En una lista de adyacencia, el consumo crece con las aristas efectivas: cada nodo de lista suma el peso (4 bytes), el destino (4 bytes) y el puntero (8 bytes en arquitecturas de 64 bits), más la estructura base.

3.5 Cuándo conviene usar cada una

• Matriz: grafos densos, tamaño moderado y consultas frecuentes de adyacencia; útil para algoritmos basados en matrices (Floyd-Warshall).
• Lista: grafos dispersos o grandes, cuando se prioriza memoria o se recorre a menudo la vecindad; natural para Dijkstra con montículo y BFS/DFS.
• En proyectos mixtos se combina: matriz para precálculos rápidos y lista para recorridos eficientes.