4 - Insertion Sort

Insertion Sort ordena construyendo una sublista ordenada desde el inicio de la lista y ubicando cada nuevo elemento en su posición correcta. Es intuitivo, similar a acomodar cartas en la mano, y funciona muy bien cuando los datos ya están casi ordenados.

4.1 Idea general del algoritmo

Partimos de la premisa de que el primer elemento ya está ordenado. Luego avanzamos elemento por elemento, insertando cada valor en la posición adecuada dentro de la porción izquierda que ya está ordenada.

4.2 Concepto de sublista ordenada

Despues de cada iteración, la sección valores[0..i] queda ordenada. El resto de la lista permanece pendiente de ordenar.

4.3 Inserción en su posición correcta

Para insertar un elemento, primero buscamos dónde debe ubicarse y luego desplazamos a la derecha los elementos mayores para abrir un hueco.

4.4 Búsqueda de la posición de inserción

Comparamos el elemento actual con los de la sublista ordenada moviéndonos hacia la izquierda. Cuando encontramos uno menor o igual, sabemos que la posición es inmediatamente después.

4.5 Desplazamiento de elementos

Cada elemento mayor al valor que insertamos se mueve una posición a la derecha. Esto preserva el orden de los elementos iguales, por lo que el algoritmo es estable.

4.6 Implementación en Python

Versión clásica para enteros. Usa un bucle externo que recorre cada elemento y un bucle interno que desplaza hasta encontrar la posición correcta.

def insertion_sort(valores):
  for i in range(1, len(valores)):
    actual = valores[i]
    j = i - 1
    while j >= 0 and valores[j] > actual:
      valores[j + 1] = valores[j]
      j -= 1
    valores[j + 1] = actual

Explicación línea por línea:

• for i in range(1, len(valores)): recorre elementos desde el segundo, que es el primero que puede desplazarse.
• actual = valores[i]: guarda el valor que queremos insertar en la sublista ordenada.
• j = i - 1: arranca la comparación desde el elemento previo dentro de la sublista.
• while j >= 0 and valores[j] > actual: busca hacia la izquierda hasta hallar un elemento menor o igual; mientras sea mayor, se desplaza.
• valores[j + 1] = valores[j]: mueve el elemento mayor una posición a la derecha para hacer lugar.
• j -= 1: avanza el índice hacia la izquierda para seguir comparando.
• valores[j + 1] = actual: coloca el valor original en la posición vaciada, que es su lugar correcto.

4.7 Complejidad temporal y espacial

• Tiempo: O(n^2) en el peor caso (lista inversa); O(n) en el mejor caso cuando la lista ya está ordenada.
• Memoria: O(1) adicional; trabaja in-place.
• Estabilidad: estable por el desplazamiento ordenado hacia la derecha.

4.8 Ventajas y desventajas

• Ventajas: excelente rendimiento en listas pequeñas o casi ordenadas; estable; implementación breve y clara.
• Desventajas: su complejidad cuadrática lo limita para listas grandes; el desplazamiento puede ser costoso cuando los datos están muy desordenados.

4.9 Casos donde Insertion Sort es excelente

• Datos casi ordenados, donde el número de desplazamientos es mínimo.
• Listas pequeñas, por ejemplo, tramos cortos dentro de un algoritmo híbrido.
• Situaciones donde la estabilidad es importante y el tamaño de la entrada es acotado.

Insertion Sort suele usarse dentro de implementaciones híbridas: algoritmos más rápidos como quicksort delegan a Insertion Sort cuando la sublista es pequeña para aprovechar su simplicidad.

4.10 Archivo único de trabajo

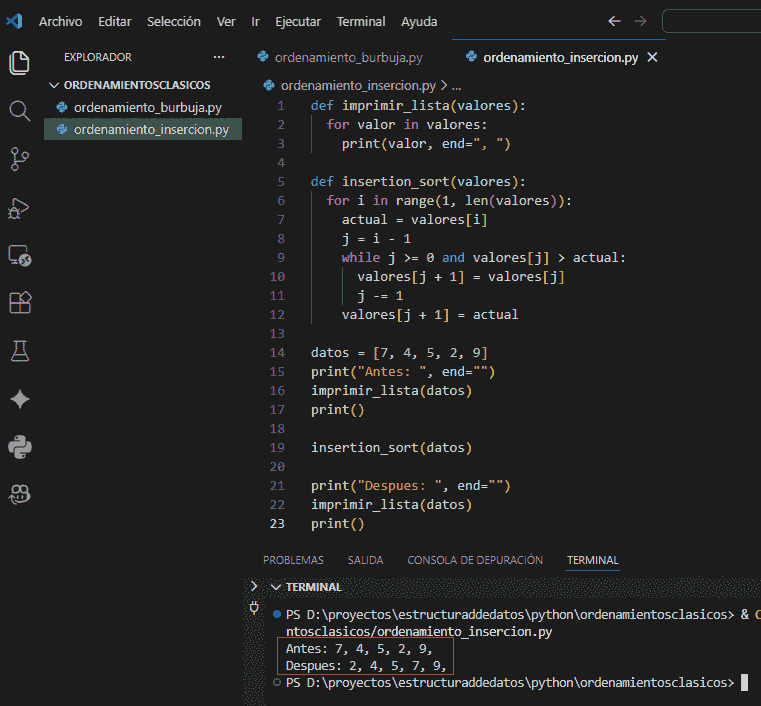
Usaremos un solo archivo con los datos de prueba y la impresión del resultado para revisar rápidamente el algoritmo.

def imprimir_lista(valores):
  for valor in valores:
    print(valor, end=", ")

def insertion_sort(valores):
  for i in range(1, len(valores)):
    actual = valores[i]
    j = i - 1
    while j >= 0 and valores[j] > actual:
      valores[j + 1] = valores[j]
      j -= 1
    valores[j + 1] = actual

datos = [7, 4, 5, 2, 9]
print("Antes: ", end="")
imprimir_lista(datos)
print()

insertion_sort(datos)

print("Despues: ", end="")
imprimir_lista(datos)
print()