5 - Selection Sort

Selection Sort ordena seleccionando el mínimo (o máximo) restante en cada pasada y colocándolo en su posición definitiva. Realiza pocos intercambios, lo que puede ser ventajoso cuando el costo de swap es alto.

5.1 Idea general del algoritmo

En cada iteración externa, se asume que la sección izquierda ya está ordenada. Se busca el elemento más pequeño en la parte no ordenada y se lo intercambia con el elemento en la posición actual.

5.2 Búsqueda del mínimo en el resto de la lista

El recorrido interno localiza el índice del mínimo desde la posición siguiente a la actual hasta el final de la lista.

5.3 Intercambio con la posición actual

Una vez identificado el mínimo, se lo intercambia con la posición actual. Si ya está en el lugar correcto, el swap no es necesario.

5.4 Recorrido externo y recorrido interno

El bucle externo avanza la frontera de la zona ordenada. El bucle interno recorre el segmento restante para encontrar el mínimo.

5.5 Implementación en Python

Versión clásica para orden ascendente; utiliza la función swap ya definida.

def swap(valores, i, j):
  valores[i], valores[j] = valores[j], valores[i]

def selection_sort(valores):
  for i in range(len(valores) - 1):
    indice_min = i
    for j in range(i + 1, len(valores)):
      if valores[j] < valores[indice_min]:
        indice_min = j
    if indice_min != i:
      swap(valores, i, indice_min)

Explicación línea por línea:

• for i in range(len(valores) - 1): define la posición donde colocar el siguiente mínimo.
• indice_min = i: asume que el mínimo inicial está en la posición actual.
• for j in range(i + 1, len(valores)): busca el mínimo real en el resto de la lista.
• if valores[j] < valores[indice_min]: indice_min = j: actualiza el índice del mínimo cuando encuentra un valor menor.
• if indice_min != i: swap(valores, i, indice_min): intercambia solo si el mínimo no está ya en su lugar.

5.6 Complejidad temporal y espacial

• Tiempo: O(n^2) en todos los casos; el número de comparaciones es constante para un tamaño dado.
• Memoria: O(1) adicional; trabaja in-place.
• Estabilidad: no es estable porque un swap puede cambiar el orden relativo de elementos iguales.

5.7 Ventajas y desventajas

• Ventajas: pocos intercambios (a lo sumo n - 1); implementación sencilla; rendimiento predecible.
• Desventajas: complejidad cuadrática incluso si la lista ya está ordenada; no es estable.

5.8 Casos donde Selection Sort es útil

• Cuando el costo del swap es alto pero comparar es barato.
• Listas pequeñas donde la simplicidad prima sobre el rendimiento asintótico.
• Escenarios educativos o de depuración para contrastar resultados con otros algoritmos.

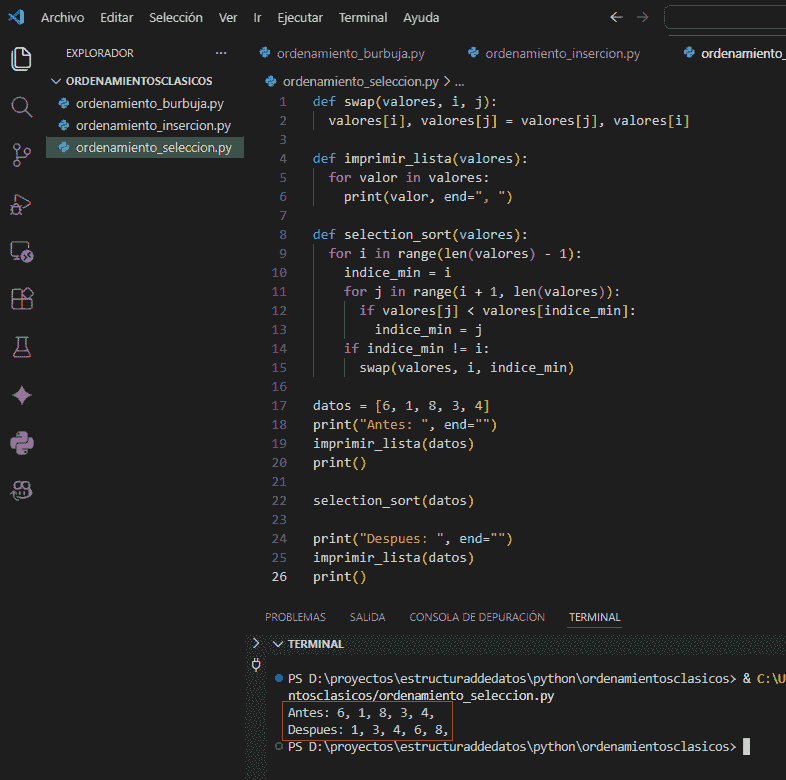
5.9 Archivo único de trabajo

Usaremos un solo archivo con datos de prueba y la impresión del resultado.

def swap(valores, i, j):
  valores[i], valores[j] = valores[j], valores[i]

def imprimir_lista(valores):
  for valor in valores:
    print(valor, end=", ")

def selection_sort(valores):
  for i in range(len(valores) - 1):
    indice_min = i
    for j in range(i + 1, len(valores)):
      if valores[j] < valores[indice_min]:
        indice_min = j
    if indice_min != i:
      swap(valores, i, indice_min)

datos = [6, 1, 8, 3, 4]
print("Antes: ", end="")
imprimir_lista(datos)
print()

selection_sort(datos)

print("Despues: ", end="")
imprimir_lista(datos)
print()