3 - MergeSort

MergeSort es un ordenamiento eficiente basado en división y conquista. Divide el array en mitades, ordena cada parte de forma recursiva y luego las combina manteniendo el orden. Con complejidad O(n log n) y estabilidad, es la opción preferida en escenarios donde la consistencia del orden importa.

3.1 Idea general: dividir, ordenar, mergear

MergeSort crea un árbol binario de subproblemas:

• Divide el array en dos mitades hasta llegar a subarrays de un elemento.
• Ordena cada mitad de forma recursiva.
• Fusiona las dos mitades ordenadas en un solo array ordenado.

3.2 División recursiva del array

La clave está en partir el problema a la mitad hasta llegar al caso base:

void mergesort(int *valores, int inicio, int fin) {
  if (inicio >= fin) {
    return;
  }
  int medio = (inicio + fin) / 2;
  mergesort(valores, inicio, medio);
  mergesort(valores, medio + 1, fin);
  merge(valores, inicio, medio, fin);
}

Cada llamada recursiva trabaja sobre un rango definido por índices inclusivos.

3.3 Función merge()

La función de mezcla toma dos mitades ordenadas y produce una salida ordenada en un buffer auxiliar, luego copia el resultado al array original:

#include <stdlib.h>

void merge(int *valores, int inicio, int medio, int fin) {
  int total = fin - inicio + 1;
  int *buffer = malloc(sizeof(int) * total);
  if (!buffer) {
    return; /* degradar sin crashear si la reserva falla */
  }

  int i = inicio;
  int j = medio + 1;
  int k = 0;

  while (i <= medio && j <= fin) {
    if (valores[i] <= valores[j]) {
      buffer[k++] = valores[i++];
    } else {
      buffer[k++] = valores[j++];
    }
  }
  while (i <= medio) {
    buffer[k++] = valores[i++];
  }
  while (j <= fin) {
    buffer[k++] = valores[j++];
  }
  for (int t = 0; t < total; t++) {
    valores[inicio + t] = buffer[t];
  }
  free(buffer);
}

El tamaño del buffer siempre coincide con el segmento a mezclar, evitando desbordes y manteniendo la estabilidad.

3.4 Ordenamiento estable

MergeSort preserva el orden relativo de elementos equivalentes porque al mezclar toma primero el elemento de la izquierda cuando son iguales (<= en la comparación). Esta propiedad es clave en reportes, agrupaciones y operaciones de deduplicación.

3.5 Uso de memoria adicional (O(n))

La mezcla necesita espacio auxiliar proporcional al tamaño del segmento a combinar. En entornos críticos de memoria es común reutilizar un buffer global o alternar entre dos arrays para reducir copias.

3.6 Implementación recursiva en C

Para evitar reservar y liberar memoria en cada mezcla, usamos un buffer auxiliar reutilizable:

#include <stdlib.h>

static void merge_with_buffer(int *arr, int *buffer, int inicio, int medio, int fin) {
  int i = inicio;
  int j = medio + 1;
  int k = inicio;
  while (i <= medio && j <= fin) {
    if (arr[i] <= arr[j]) {
      buffer[k++] = arr[i++];
    } else {
      buffer[k++] = arr[j++];
    }
  }
  while (i <= medio) {
    buffer[k++] = arr[i++];
  }
  while (j <= fin) {
    buffer[k++] = arr[j++];
  }
  for (int t = inicio; t <= fin; t++) {
    arr[t] = buffer[t];
  }
}

static void mergesort_rec(int *arr, int *buffer, int inicio, int fin) {
  if (inicio >= fin) {
    return;
  }
  int medio = (inicio + fin) / 2;
  mergesort_rec(arr, buffer, inicio, medio);
  mergesort_rec(arr, buffer, medio + 1, fin);
  merge_with_buffer(arr, buffer, inicio, medio, fin);
}

El buffer se pasa a todas las llamadas y se escribe el resultado ordenado directamente en el array original.

3.7 MergeSort "top-down"

La versión recursiva clásica reserva el buffer una sola vez y lo comparte:

void mergesort_topdown(int *arr, int n) {
  int *buffer = malloc(sizeof(int) * n);
  if (!buffer) {
    return;
  }
  mergesort_rec(arr, buffer, 0, n - 1);
  free(buffer);
}

Esta estrategia reduce la sobrecarga de reservas y mantiene la estabilidad del algoritmo.

3.8 MergeSort "bottom-up" (iterativo)

La variante iterativa evita recursión. Recorre el array en runs de tamaño creciente y mezcla pares adyacentes:

void mergesort_bottomup(int *arr, int n) {
  for (int size = 1; size < n; size *= 2) {
    for (int inicio = 0; inicio < n - size; inicio += 2 * size) {
      int medio = inicio + size - 1;
      int fin = (inicio + 2 * size - 1 < n) ? inicio + 2 * size - 1 : n - 1;
      merge(arr, inicio, medio, fin);
    }
  }
}

Resulta práctico cuando se desea controlar el consumo de pila o instrumentar el algoritmo paso a paso. Para minimizar reservas, se puede usar un buffer compartido igual que en la versión top-down.

3.9 Complejidad temporal y espacial

• Tiempo: O(n log n) en peor, promedio y mejor caso.
• Memoria: O(n) espacio adicional para el buffer de mezcla.
• Estabilidad: estable siempre que la mezcla respete el orden de iguales.

3.10 Ventajas y desventajas

• Ventajas: complejidad garantizada O(n log n) incluso en el peor caso; estabilidad; buen comportamiento en datos parcialmente ordenados; estructura clara para paralelizar la fase de división.
• Desventajas: requiere memoria adicional; las copias pueden impactar en caché; no es in-place salvo optimizaciones avanzadas.

3.11 Casos ideales de uso

• Listas enormes: garantiza rendimiento y estabilidad sin sorpresas en el peor caso.
• Datos parcialmente ordenados: la mezcla aprovecha runs existentes y mantiene el orden relativo.
• Ordenamiento externo: la estrategia de mezcla secuencial se adapta bien a archivos y flujos.

MergeSort es un punto de partida excelente para comprender ordenamientos eficientes: muestra cómo dividir y combinar de forma sistemática y establece un rendimiento predecible.

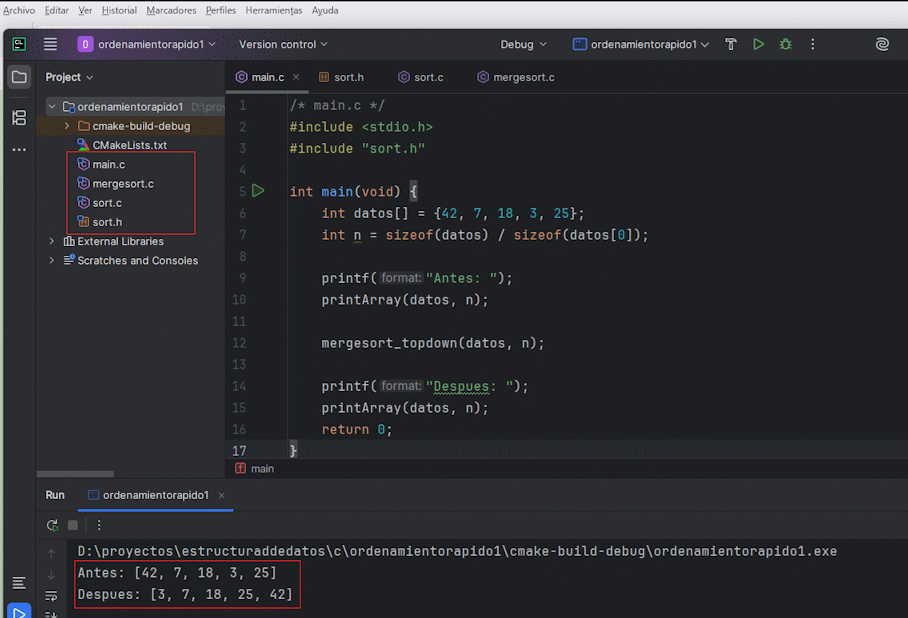
3.12 Archivos indispensables para un proyecto en CLion

Estructura mínima para compilar y depurar MergeSort en CLion o desde consola. Incluye el código de cada archivo base:

/* sort.h */
void merge(int *valores, int inicio, int medio, int fin);
void mergesort_topdown(int *arr, int n);
void printArray(const int *arr, int n);

/* sort.c */
#include <stdio.h>
#include <stdlib.h>
#include "sort.h"

void printArray(const int *arr, int n) {
  printf("[");
  for (int i = 0; i < n; i++) {
    printf("%d", arr[i]);
    if (i + 1 < n) {
      printf(", ");
    }
  }
  printf("]\n");
}

void merge(int *valores, int inicio, int medio, int fin) {
  int total = fin - inicio + 1;
  int *buffer = malloc(sizeof(int) * total);
  if (!buffer) {
    return;
  }
  int i = inicio;
  int j = medio + 1;
  int k = 0;
  while (i <= medio && j <= fin) {
    if (valores[i] <= valores[j]) {
      buffer[k++] = valores[i++];
    } else {
      buffer[k++] = valores[j++];
    }
  }
  while (i <= medio) {
    buffer[k++] = valores[i++];
  }
  while (j <= fin) {
    buffer[k++] = valores[j++];
  }
  for (int t = 0; t < total; t++) {
    valores[inicio + t] = buffer[t];
  }
  free(buffer);
}

/* mergesort.c */
#include <stdlib.h>
#include "sort.h"

static void merge_with_buffer(int *arr, int *buffer, int inicio, int medio, int fin) {
  int i = inicio;
  int j = medio + 1;
  int k = inicio;
  while (i <= medio && j <= fin) {
    if (arr[i] <= arr[j]) {
      buffer[k++] = arr[i++];
    } else {
      buffer[k++] = arr[j++];
    }
  }
  while (i <= medio) {
    buffer[k++] = arr[i++];
  }
  while (j <= fin) {
    buffer[k++] = arr[j++];
  }
  for (int t = inicio; t <= fin; t++) {
    arr[t] = buffer[t];
  }
}

static void mergesort_rec(int *arr, int *buffer, int inicio, int fin) {
  if (inicio >= fin) {
    return;
  }
  int medio = (inicio + fin) / 2;
  mergesort_rec(arr, buffer, inicio, medio);
  mergesort_rec(arr, buffer, medio + 1, fin);
  merge_with_buffer(arr, buffer, inicio, medio, fin);
}

void mergesort_topdown(int *arr, int n) {
  int *buffer = malloc(sizeof(int) * n);
  if (!buffer) {
    return;
  }
  mergesort_rec(arr, buffer, 0, n - 1);
  free(buffer);
}

/* main.c */
#include <stdio.h>
#include "sort.h"

int main(void) {
  int datos[] = {42, 7, 18, 3, 25};
  int n = sizeof(datos) / sizeof(datos[0]);

  printf("Antes: ");
  printArray(datos, n);

  mergesort_topdown(datos, n);

  printf("Despues: ");
  printArray(datos, n);
  return 0;
}

Con esta separación, CLion recompila solo los archivos modificados y puedes hacer step-by-step en cada fase del algoritmo.