4 - QuickSort

QuickSort es uno de los ordenamientos más usados en la práctica por su eficiencia promedio O(n log n) y su bajo uso de memoria. Funciona al elegir un pivote, particionar el array en torno a él y ordenar recursivamente las particiones.

4.1 Idea general: pivote y particiones

El pivote define un punto de corte: todos los elementos menores (o iguales) quedan a su izquierda y los mayores a su derecha. Luego QuickSort se aplica recursivamente a cada lado hasta que los subarrays sean de tamaño 0 o 1.

4.2 Estrategias para elegir pivote

• Primer elemento: simple pero vulnerable a datos ya ordenados.
• Último elemento: igual de simple, también expuesto a peores casos.
• Aleatorio: reduce la probabilidad de peores casos sistemáticos.
• Mediana de tres: calcula la mediana entre primero, medio y último; suele mejorar la calidad del pivote con bajo costo.

4.3 Particionamiento: esquemas clásicos

Los dos esquemas más usados son Lomuto y Hoare. Lomuto es más simple; Hoare reduce intercambios.

/* Particionamiento de Lomuto */
int particion_lomuto(int *arr, int inicio, int fin) {
  int pivote = arr[fin];
  int i = inicio - 1;
  for (int j = inicio; j < fin; j++) {
    if (arr[j] <= pivote) {
      i++;
      int tmp = arr[i];
      arr[i] = arr[j];
      arr[j] = tmp;
    }
  }
  int tmp = arr[i + 1];
  arr[i + 1] = arr[fin];
  arr[fin] = tmp;
  return i + 1;
}

/* Particionamiento de Hoare */
int particion_hoare(int *arr, int inicio, int fin) {
  int pivote = arr[(inicio + fin) / 2];
  int i = inicio - 1;
  int j = fin + 1;
  while (1) {
    do { i++; } while (arr[i] < pivote);
    do { j--; } while (arr[j] > pivote);
    if (i >= j) {
      return j; /* devuelve el índice que separa las particiones */
    }
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
  }
}

4.4 Recursión en subarrays izquierdo y derecho

Tras particionar, se invoca QuickSort sobre cada lado. El esquema de llamada cambia según la función de partición:

void quicksort_lomuto(int *arr, int inicio, int fin) {
  if (inicio >= fin) {
    return;
  }
  int p = particion_lomuto(arr, inicio, fin);
  quicksort_lomuto(arr, inicio, p - 1);
  quicksort_lomuto(arr, p + 1, fin);
}

void quicksort_hoare(int *arr, int inicio, int fin) {
  if (inicio >= fin) {
    return;
  }
  int p = particion_hoare(arr, inicio, fin);
  quicksort_hoare(arr, inicio, p);
  quicksort_hoare(arr, p + 1, fin);
}

4.5 Implementación en C

Versión completa usando mediana de tres y partición de Lomuto:

static int mediana_de_tres(int *arr, int inicio, int fin) {
  int medio = (inicio + fin) / 2;
  if (arr[medio] < arr[inicio]) {
    int tmp = arr[medio]; arr[medio] = arr[inicio]; arr[inicio] = tmp;
  }
  if (arr[fin] < arr[inicio]) {
    int tmp = arr[fin]; arr[fin] = arr[inicio]; arr[inicio] = tmp;
  }
  if (arr[fin] < arr[medio]) {
    int tmp = arr[fin]; arr[fin] = arr[medio]; arr[medio] = tmp;
  }
  return medio;
}

int particion_lomuto_mediana(int *arr, int inicio, int fin) {
  int m = mediana_de_tres(arr, inicio, fin);
  int tmp = arr[m]; arr[m] = arr[fin]; arr[fin] = tmp; /* mover pivote al final */
  int pivote = arr[fin];
  int i = inicio - 1;
  for (int j = inicio; j < fin; j++) {
    if (arr[j] <= pivote) {
      i++;
      int swap = arr[i];
      arr[i] = arr[j];
      arr[j] = swap;
    }
  }
  int swap = arr[i + 1];
  arr[i + 1] = arr[fin];
  arr[fin] = swap;
  return i + 1;
}

void quicksort(int *arr, int inicio, int fin) {
  if (inicio >= fin) {
    return;
  }
  int p = particion_lomuto_mediana(arr, inicio, fin);
  quicksort(arr, inicio, p - 1);
  quicksort(arr, p + 1, fin);
}

4.6 Complejidad temporal

• Caso promedio: O(n log n) gracias a particiones balanceadas en expectativa.
• Peor caso: O(n^2) cuando el pivote genera particiones muy desbalanceadas (datos ya ordenados con pivote fijo).

4.7 Cómo evitar el peor caso

• Elegir pivote aleatorio o mediana de tres reduce la probabilidad de caer en particiones extremas.
• Alternar a Insertion Sort en subarrays pequeños (<= 16) mejora las constantes y evita recursiones profundas.
• Limitar la profundidad de recursión y caer a HeapSort si se supera un umbral (estrategia introsort).

4.8 Ventajas y desventajas

• Ventajas: muy rápido en promedio; trabaja in-place con O(1) memoria extra; fácil de adaptar a distintos tipos de datos.
• Desventajas: peor caso cuadrático si el pivote es deficiente; no es estable; puede consumir mucha pila en entradas adversas.

4.9 Casos de uso ideales

• Arrays grandes: in-place y con buenas constantes en memoria caché.
• Datos sin requerimiento de estabilidad: rankings, ordenamientos de IDs, estructuras temporales.
• Algoritmos híbridos: base para introsort o conmutación a Insertion Sort en tramos cortos.

QuickSort sigue siendo la opción por defecto en muchas librerías gracias a su rendimiento promedio y bajo consumo de memoria.

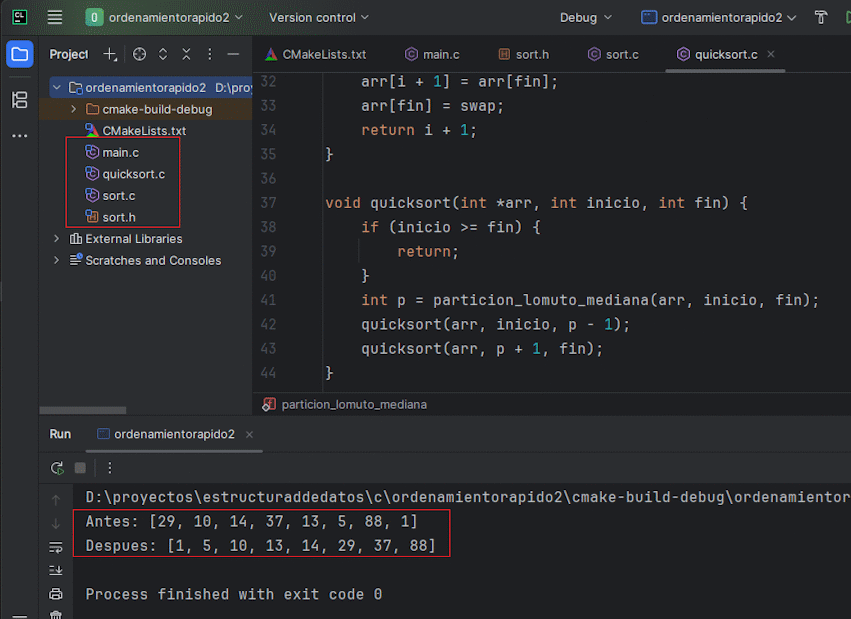
4.10 Archivos indispensables para un proyecto en CLion

Estructura mínima con código listo para compilar y probar QuickSort:

/* sort.h */
void quicksort(int *arr, int inicio, int fin);
void printArray(const int *arr, int n);

/* sort.c */
#include <stdio.h>
#include "sort.h"

void printArray(const int *arr, int n) {
  printf("[");
  for (int i = 0; i < n; i++) {
    printf("%d", arr[i]);
    if (i + 1 < n) {
      printf(", ");
    }
  }
  printf("]\n");
}

/* quicksort.c */
#include "sort.h"

static int mediana_de_tres(int *arr, int inicio, int fin) {
  int medio = (inicio + fin) / 2;
  if (arr[medio] < arr[inicio]) {
    int tmp = arr[medio]; arr[medio] = arr[inicio]; arr[inicio] = tmp;
  }
  if (arr[fin] < arr[inicio]) {
    int tmp = arr[fin]; arr[fin] = arr[inicio]; arr[inicio] = tmp;
  }
  if (arr[fin] < arr[medio]) {
    int tmp = arr[fin]; arr[fin] = arr[medio]; arr[medio] = tmp;
  }
  return medio;
}

static int particion_lomuto_mediana(int *arr, int inicio, int fin) {
  int m = mediana_de_tres(arr, inicio, fin);
  int tmp = arr[m]; arr[m] = arr[fin]; arr[fin] = tmp;
  int pivote = arr[fin];
  int i = inicio - 1;
  for (int j = inicio; j < fin; j++) {
    if (arr[j] <= pivote) {
      i++;
      int swap = arr[i];
      arr[i] = arr[j];
      arr[j] = swap;
    }
  }
  int swap = arr[i + 1];
  arr[i + 1] = arr[fin];
  arr[fin] = swap;
  return i + 1;
}

void quicksort(int *arr, int inicio, int fin) {
  if (inicio >= fin) {
    return;
  }
  int p = particion_lomuto_mediana(arr, inicio, fin);
  quicksort(arr, inicio, p - 1);
  quicksort(arr, p + 1, fin);
}

/* main.c */
#include <stdio.h>
#include "sort.h"

int main(void) {
  int datos[] = {29, 10, 14, 37, 13, 5, 88, 1};
  int n = sizeof(datos) / sizeof(datos[0]);

  printf("Antes: ");
  printArray(datos, n);

  quicksort(datos, 0, n - 1);

  printf("Despues: ");
  printArray(datos, n);
  return 0;
}

Con esta base puedes intercambiar el esquema de pivote o la función de partición sin cambiar la interfaz pública.