12 - Ejemplo práctico 3: backtracking en un laberinto

12.1 Formulación del problema

Tenemos un laberinto rectangular representado como una matriz de caracteres donde # son paredes, . celdas transitables, S el inicio y E la salida. Debemos encontrar un camino sin recursión, usando una pila para recordar las posiciones visitadas y retroceder cuando no haya movimientos disponibles.

12.2 Estructura de datos

  • Una pila que almacena coordenadas (fila, columna).
  • Una matriz auxiliar de visitados para evitar bucles.
  • Un arreglo con los cuatro movimientos posibles: arriba, abajo, izquierda, derecha.

12.3 Flujo del algoritmo

  1. Apilar la posición de inicio.
  2. Mientras la pila no esté vacía:
    • Consultar el tope.
    • Si es la salida, detenerse.
    • Buscar el siguiente vecino no visitado; si existe, marcarlo, apilarlo y continuar.
    • Si no hay vecinos, desapilar (backtracking).

El algoritmo es un DFS iterativo basado en pila.

12.4 Casos especiales

  • Laberintos sin salida: la pila terminará vacía sin hallar E.
  • Múltiples salidas: se detiene en la primera encontrada; se puede continuar para encontrar todas.
  • Restricciones de movimiento (diagonal, portales) pueden modelarse agregando direcciones extra.

12.5 Implementación en C

#include <stdio.h>

#define MAX 8

typedef struct {
  int fila;
  int col;
} Pos;

typedef struct {
  Pos datos[MAX * MAX];
  int top;
} PilaPos;

void pila_init(PilaPos *p) { p->top = 0; }
int pila_is_empty(const PilaPos *p) { return p->top == 0; }
void pila_push(PilaPos *p, Pos pos) { p->datos[p->top++] = pos; }
Pos pila_pop(PilaPos *p) { return p->datos[--p->top]; }
Pos pila_peek(const PilaPos *p) { return p->datos[p->top - 1]; }

int dentro(int fila, int col, int filas, int cols) {
  return fila >= 0 && fila < filas && col >= 0 && col < cols;
}

int resolver(char mapa[MAX][MAX], int filas, int cols) {
  PilaPos pila;
  pila_init(&pila);
  int visitado[MAX][MAX] = {0};
  Pos start = {-1, -1};
  for (int i = 0; i < filas; ++i)
    for (int j = 0; j < cols; ++j)
      if (mapa[i][j] == 'S') start = (Pos){i, j};

  if (start.fila == -1) return 0;
  pila_push(&pila, start);
  visitado[start.fila][start.col] = 1;

  const int movs[4][2] = {{-1,0},{1,0},{0,-1},{0,1}};

  while (!pila_is_empty(&pila)) {
    Pos actual = pila_peek(&pila);
    if (mapa[actual.fila][actual.col] == 'E') return 1;

    int avanzo = 0;
    for (int k = 0; k < 4; ++k) {
      int nf = actual.fila + movs[k][0];
      int nc = actual.col + movs[k][1];
      if (!dentro(nf, nc, filas, cols)) continue;
      if (mapa[nf][nc] == '#' || visitado[nf][nc]) continue;
      visitado[nf][nc] = 1;
      pila_push(&pila, (Pos){nf, nc});
      avanzo = 1;
      break;
    }
    if (!avanzo) pila_pop(&pila); /* retrocede */
  }
  return 0;
}

int main(void) {
  char lab[MAX][MAX] = {
    "S....#..",
    "##.#.#..",
    "..#....E",
    "..#....#",
    "..#####.",
    "..#.....",
    "..###.##",
    "........"
  };

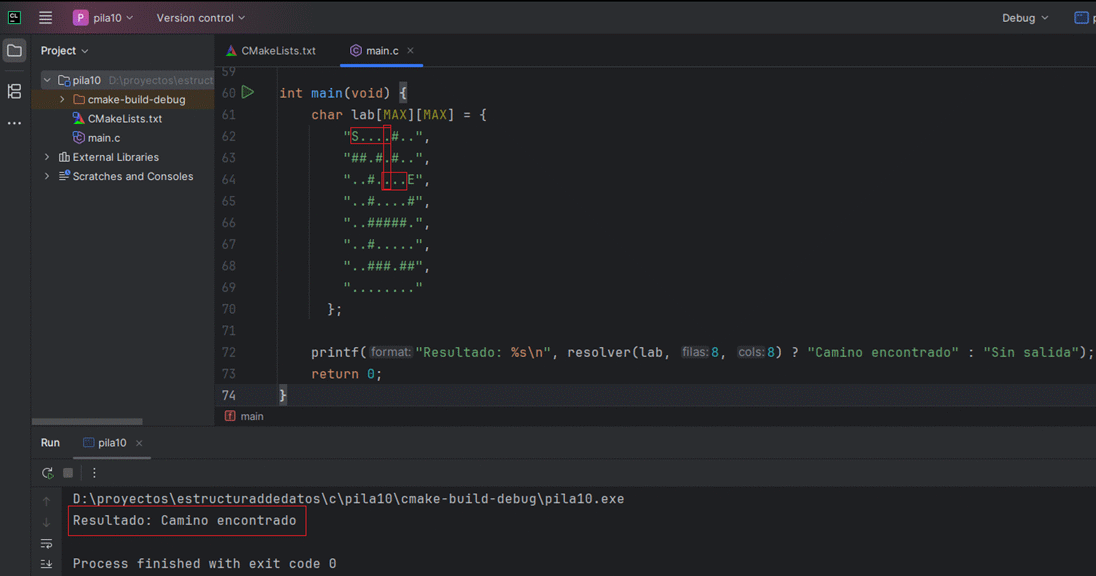
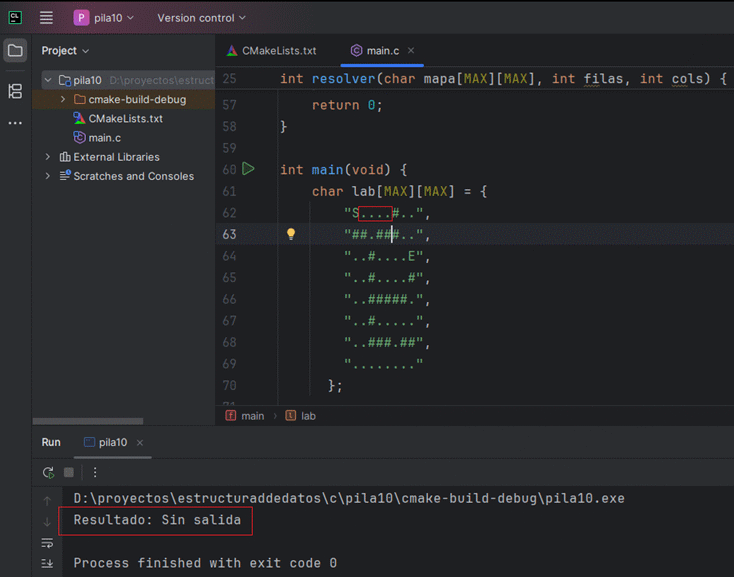
  printf("Resultado: %s\n", resolver(lab, 8, 8) ? "Camino encontrado" : "Sin salida");
  return 0;
}

Este ejemplo usa un tablero pequeño, pero la lógica escala a mapas grandes cambiando las constantes.

Representación del laberinto resuelto con pilas Ilustración del camino encontrado

12.6 Extensiones y entrevistas

  • Registrar el camino final copiando la pila en un arreglo auxiliar.
  • Agregar pesos o recolectar objetos en el recorrido.
  • Convertir el algoritmo a una pila de listas para guardar decisiones en juegos de backtracking, muy popular en entrevistas de algoritmos.
Retornar